922 . 轉椅子好好玩
Description
本題為互動題,限用 C++ 作答。你可以在這裡找到範例實作以及範例評分程式,詳細注意事項以及常見問題請參考 Hints。
當波路特石站在一堆旋轉椅的地方時,他會用手不斷地旋轉這些椅子來促進他思考。有一天,他實在是懶到不想移動,懶到他只願意待在一個凸多邊形 $A$ 的範圍內,並撿起了身邊的一根棍子打算用它來旋轉椅子,可以見範例影片。
為了旋轉椅子,波路特石會找到 $A$ 的其中一個頂點站定位,再試圖用棍子去戳椅子的邊邊,好讓椅子順時針旋轉。不過為了簡化問題,我們假設椅子是另一個凸多邊形 $B$,並且波路特石會選定在其身上的一條邊當做旋轉基準,以下圖為範例:
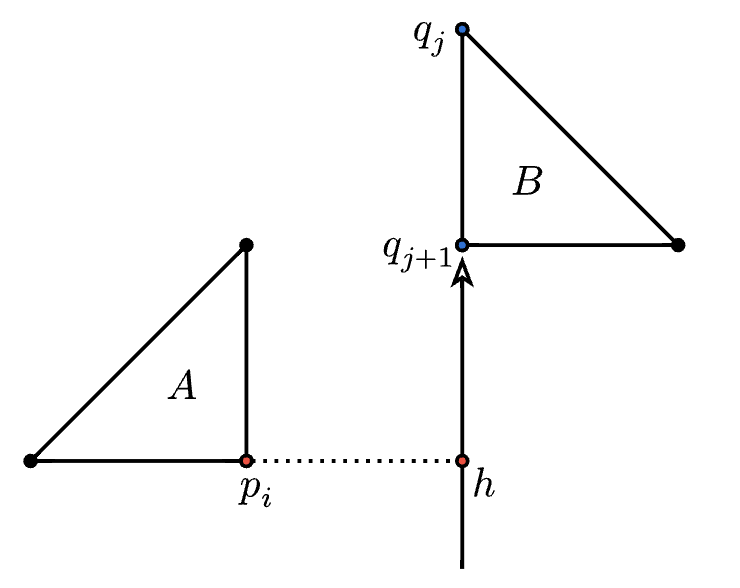
在上圖中,波路特石站在凸多邊形 $A$ 的頂點 $p_i$,並選擇凸多邊形 $B$ 的邊 $\overline{q_{j}q_{j+1}}$ 當作旋轉基準後,拿著棍子使用與 $\overline{q_{j}q_{j+1}}$ 在平行的角度戳 $q_{j+1}$ 這個點來讓椅子順時針旋轉。
不過,波路特石發現手伸太長會很累,他發現,這個勞累程度會正比於他站的定點到選定邊形成直線的垂直距離,以上圖的例子就是 $p_i$ 到 $\overline{q_{j}q_{j+1}}$ 延長線的垂點 $h$、所形成線段 $\overline{p_ih}$ 的長度,當這個值越小,波路特石就覺得他轉起椅子來越輕鬆。因此,你必須完成兩個任務:
- 任務一:你得實作出一個函式,在當波路特石詢問你一個站點 $p$、一條邊 $\overline{q_1q_2}$ 時,你都能回答出一個整數估計值,使得該估計值在固定 $\overline{q_1q_2}$ 的情況下,該值會正比於 $p$ 到 $\overline{q_1q_2}$ 的有向距離。而所謂有向距離,代表的是當要站在頂點 $p$ 戳 $q_2$ 這個點來旋轉椅子時,可能會需要使用正手、突刺或是反手的方式旋轉。注意到因為波路特石要讓椅子順時針旋轉,因此當要戳邊 $\overline{q_1q_2}$ 時,他一定得戳點 $q_2$ 來旋轉椅子,這唯一決定了使用正手、突刺還是反手的時機,可以參考下圖來了解:
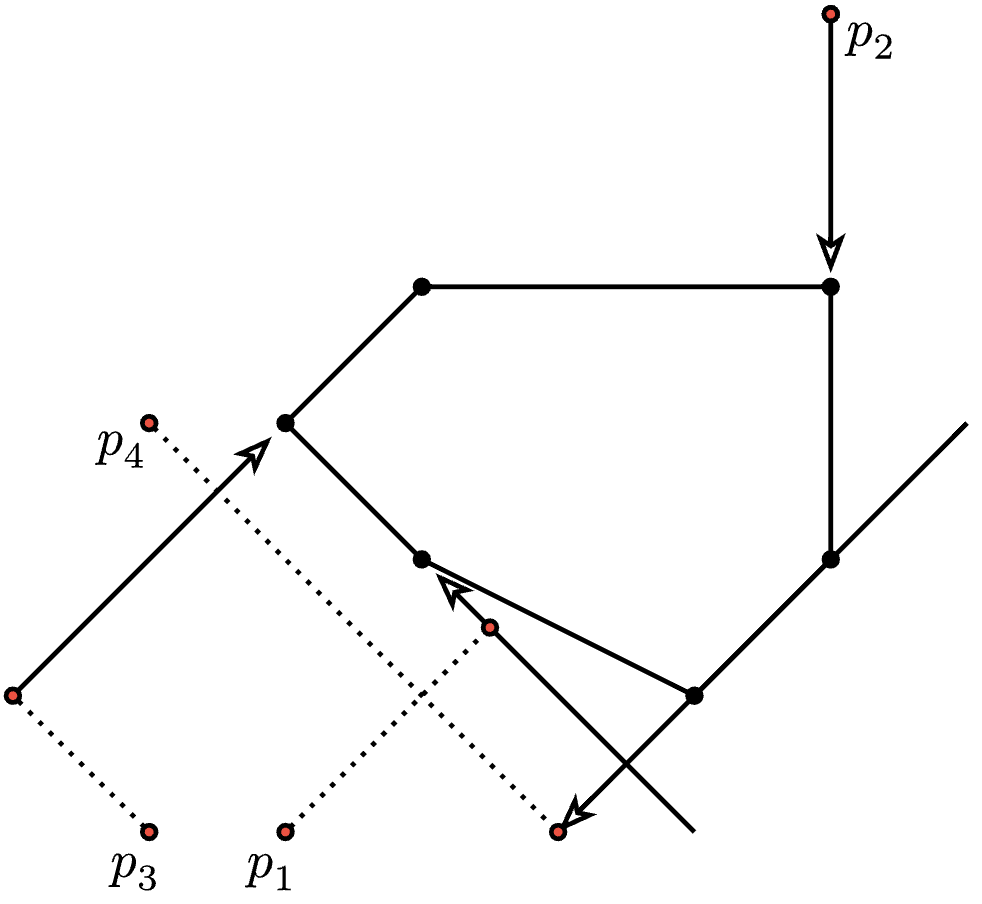
根據我們的定義,當旋轉的方式是正手時,垂直距離為正;當旋轉的方式是突刺時,垂直距離為零;當旋轉的方式是反手時,垂直距離為負。而上圖中的 $p_1, p_2, p_3$ 分別就提供了順時針旋轉中間凸多邊形時,需要使用正手、突刺還是反手的範例。$p_4$ 作為一個較為迥異的範例,當站在 $p_4$ 時,波路特石得戳比較外側的點才能讓凸多邊形順時針旋轉,儘管很難想像他會用什麼姿勢達成這項創舉,你可以假設他總是辦得到,一樣使用對應的垂直距離來幫他估計即可,當然,這個距離為負,因為他得使用反手的方式來旋轉。前面範例影片則是提供了一個正手旋轉的範例。
- 任務二:波路特石希望,對於凸多邊形 $B$ 的每一條邊,你都能夠告訴他在最糟情況下,這個旋轉椅子的估計值絕對值會有多大,好讓波路特石迴避那些旋轉起來會特別累的邊。而這裡的估計值,就是你在任務一回傳的值。具體來說,你必須實作一支函式,在僅得知 $A$ 與 $B$ 點數的情況下,盡量少次地估計波路特石站在 $A$ 的指定頂點 $p_i$ 到 $B$ 的指定邊 $\overline{q_{j}q_{j+1}}$ 的有向垂直距離,並回傳一個陣列來告訴波路特石 $B$ 中的每個邊可以得到的最大估計值絕對值。
詳細細節與評分方式請見後續段落。
Implementation Details
你的程式需要在一開始使用前置處理器引入 lib0922.h,詳細請參考範例實作。
你需要完成以下的兩個函式:
long long calculate_distance(int px, int py, int qx1, int qy1, int qx2, int qy2);
- 在一筆測試資料中,
calculate_distance會被呼叫至多 $750\ 000$ 次。 - 引數
px和py是波路特石的站點 $p$。 - 引數
qx1和qy1是波路特石要旋轉的邊的第一個點 $q_1$。 - 引數
qx2和qy2是波路特石要旋轉的邊的第二個點 $q_2$,也是要被用來旋轉的施力點。 - 回傳值必須為一個在
long long範圍內的整數,滿足:- 當 $\overline{q_1q_2}$ 固定時,你回傳的估計值與 $p$ 到 $\overline{q_1q_2}$ 的有向垂直距離成正比。
- 嚴謹地說,當 $\overline{q_1q_2}$ 固定時,存在一個正實數 $k$,滿足對於任的站點 $p$,令 $p$ 到 $\overline{q_1q_2}$ 的有向垂直距離是 $d$,則該回傳值為 $k\cdot d$。
- 做為再次提醒,當旋轉的方式是正手時,垂直距離為正;當旋轉的方式是突刺時,垂直距離為零;當旋轉的方式是反手時,垂直距離為負。
std::vector<long long> find_minimum_distances(int N, int M);
- 在一筆測試資料中,
find_minimum_distances會被呼叫至多 $500$ 次。 - 引數
N為凸多邊形 $A$ 的點數。 - 引數
M為凸多邊形 $B$ 的點數。 - 回傳值必須為一個長度為 $M$ 的陣列,第 $j$ 項為凸多邊形 $B$ 中,要透過邊 $\overline{q_jq_{j+1}}$ 旋轉椅子時,估計值絕對值的最大值。
你可以呼叫以下函式:
long long get_distance(int i, int j);
- 引數
i必須介於 $0\sim N - 1$ 之間,代表這次詢問要讓波路特石站在頂點 $p_i$ 進行測量。 - 引數
j必須介於 $0\sim M - 1$ 之間,代表這次詢問要讓波路特石利用邊 $\overline{q_{j}q_{j+1}}$ 來旋轉椅子。 - 回傳值是一個整數 $d$,該值將會是你在
calculate_distance估算出來的估計值。 get_distance不得被呼叫超過 $\textbf{250\ 000}$ 次。
如果任意一個條件沒有被滿足,你的程式會被判斷為 Wrong Answer 並且獲得 0 分,否則,你的程式將依照 Scoring 中的敘述評分。
Example
| 評測程式端 | 參賽者程式端 |
|---|---|
呼叫 find_minimum_distances(3, 3)。 | |
呼叫 get_distance(0, 0)。 | |
呼叫 calculate_distance(0, 0, 4, 2, 6, 2)。 | |
回傳 1。 | |
回傳 1。 | |
呼叫 get_distance(2, 0)。 | |
呼叫 calculate_distance(2, 2, 4, 2, 6, 2)。 | |
回傳 0。 | |
回傳 0。 | |
呼叫 get_distance(0, 1)。 | |
呼叫 calculate_distance(0, 0, 6, 2, 4, 4)。 | |
回傳 -4。 | |
回傳 -4。 | |
呼叫 get_distance(1, 1)。 | |
呼叫 calculate_distance(2, 0, 6, 2, 4, 4)。 | |
回傳 -3。 | |
回傳 -3。 | |
呼叫 get_distance(0, 2)。 | |
呼叫 calculate_distance(0, 0, 4, 4, 4, 2)。 | |
回傳 2。 | |
回傳 2。 | |
回傳 {1, 4, 2}。 |
注意到在該範例互動中,get_distance 的實現方式是將 calculate_distance 的結果原封不動的傳回給參賽者程式端,但在正式的評分程式中可能不是以該方式實現。
Constraints
- $3 \leq N, M \leq 500$
- 所有 $N$ 的總和不超過 $1500$。
- 所有 $M$ 的總和不超過 $1500$。
- 凸多邊形 $A$ 和 $B$ 不會相交,且保證以 $0, 1, 2, \ldots$ 編號遞增順序遍歷兩個凸多邊形的頂點皆會是逆時針順序。
- 凸多邊形 $A$ 和 $B$ 不會隨著互動過程而改變。
- 所有點座標將介於 $[-10^ 6, 10^ 6]$ 之間。
Scoring
get_distance 的次數最大值為 $q$,你的得分 $S$ 由下列方式計算:
- 如果 $q \leq 3\ 022$, $$S = 100$$
- 如果 $3\ 022 < q \leq 3\ 075$,
$$S = 100 - (q - 3022)^ {0.71}$$ - 如果 $3\ 075 < q \leq 3\ 500$,
$$S = 83 - \frac{22}{425}\cdot (q - 3075)$$ - 如果 $3\ 500 < q \leq 40\ 000$,
$$S = 61 - (q - 3500)^ {0.3}$$ - 如果 $40\ 000 < q \leq 250\ 000$,
$$S = 14$$
Input Format
範例評分程式以下列方式輸入:
首行輸入一個 $T$,代表子測試資料的數量,接著每一筆測試資料都以下列格式輸入:
- line $1$: $N$
- line $2+i (0\leq i < N)$: $p_{x, i}$ $p_{y, i}$
- line $2+N$: $M$
- line $3+N+i (0\leq i < M)$: $q_{x, i}$ $q_{y, i}$
Output Format
對於每一筆子測試資料,範例評分程式以下列方式輸出:
如果你的程式被判斷為 Accepted,範例評分程式會輸出 Accepted: q,其中 q 為呼叫 get_distance 的次數。接著輸出 $N$ 行,第 $j$ 行會是你回傳針對邊 $\overline{q_{j}q_{j+1}}$ 所得到的最大估計值絕對值。
如果你的程式被判斷為 Wrong Answer,範例評分程式會輸出 Wrong Answer: MSG,其中 MSG 以及其代表的意思為以下列表的其中一個:
invalid call:get_distance函式的呼叫不合法,也就是說,$i$ 不在 $0$ 至 $N - 1$ 的範圍內,或 $j$ 不在 $0$ 至 $M - 1$ 的範圍內。too many queries:get_distance呼叫的次數超過限制。invalid return value:find_minimum_distances回傳的陣列長度不是 $M$。
如果有多個原因,範例評分程式只會輸出任何一個。
另外請注意,範例評分程式並不會幫你檢查你回傳的任何數值是否是正確的。這同時也代表著,就算你的 calculate_distance 回傳了錯的數值,範例評分程式也不會察覺。
Sample Input 1
1 3 0 0 2 0 2 2 3 4 2 6 2 4 4
Sample Output 1
Accepted: 9 1 4 2
Hints
範例評分程式提供了一個詢問 $250\ 000$ 次的實作,但並沒有正確實作 calculate_distance 的內容,因此,只要你能夠正確補上 calculate_distance 的實作,你就能拿到基本分數。
另外,在正式的評分程式中,calculate_distance 跟 find_minimum_distances 的呼叫順序會略有不同,建議盡量只使用區域變數。若使用了全域變數,也請務必記得重設,更不要嘗試在這兩個函式內實作任何溝通技術來嘗試偷資料。
由於 Windows Defender 以及各種奇怪東西的限制,本題的範例編譯指令不提供 Windows 批次檔。編譯及測試教學請參考下列說明。
- 如果你的系統是 Linux 或 MacOS,你可以直接執行 compile.sh 編譯你的程式,編譯結果會是
chair,請直接用命令列執行該檔案。 - 如果你的系統是 Windows,你有以下的選擇:
- 本地測試時加入
#include "grader.cpp",並且以單一檔案的編譯執行方式測試,請注意這一行上傳時需要刪除,否則你會獲得一個 Compile Error。 - 將 compile.sh 的變數替換後直接於命令列執行,請注意你需要確保 g++ 在系統的環境變數 PATH 中。
- 如果你的電腦已經有 WSL (Windows Subsystem for Linux),你可以直接使用 WSL 並按照 Linux 的做法。
- 使用電腦教室的 Ubuntu(啟動時可以選擇系統)並按照 Linux 的做法。
- 本地測試時加入
Problem Source
IOICamp 2025 Day4 pD
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0 | 範例測資 | 0 |
| 2 | 0~28 | 無額外限制 | 100 |