完整題本 PDF：中文、英文、馬來文。

Git 是一個在軟體開發產業中廣泛使用的現代版本控制系統。Git 的一個關鍵功能是建立分支的能力，分支是可以合併回去的獨立開發線。這可以簡化開發過程，使得功能的平行開發可以在不互相干擾的情況下進行。

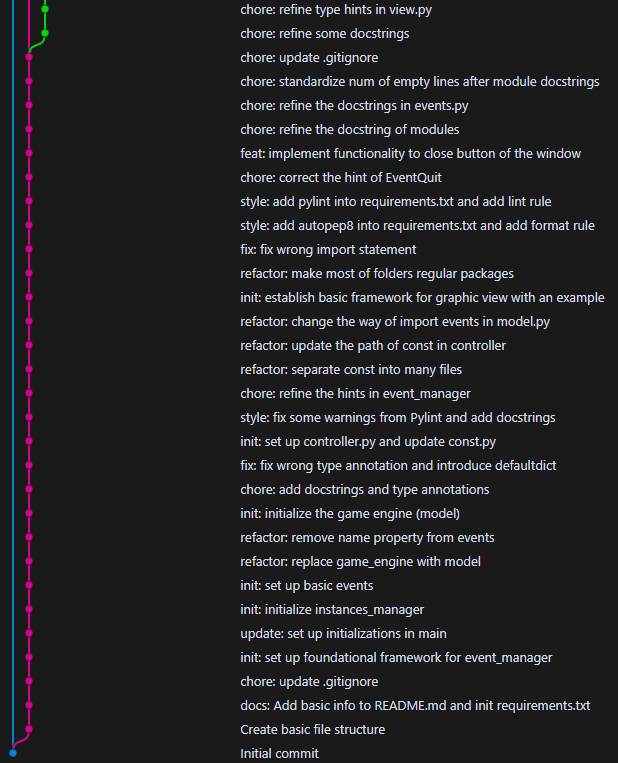
在 Git 儲存庫中，為了編輯程式碼庫，開發者建立提交（commit）來記錄他們所做的更改。提交是程式碼庫在某個時間點的快照。更重要的是，除了初始提交之外的所有提交還會記錄父提交的 ID。如果儲存庫的歷史是簡單且線性的，這會形成一條鏈。

然而，在更複雜的儲存庫中，不同的開發者在不同的功能上工作可能會編輯相同的檔案。在這種情況下，他們應該建立分支以避免他們的編輯互相干擾。當一筆新提交的父提交已經有 \textit{後代} 的話，就會自動建立分支。這也會導致一個提交成為多個提交的父提交。

在有分支的儲存庫中，開發者應該只在將分支合併回去時一次處理衝突。這會建立一種稱為合併提交的特殊類型提交。合併提交會有兩個父提交。

如你所見，要了解儲存庫的歷史，繪製圖表是視覺化歷史的好方法。為了區分不同分支的歷史，我們可以用不同的顏色為不同分支的節點著色。我們可以說，如果一個分支已經合併到另一個分支，則該分支是死亡的。另外，在圖的右下角（紅色的線）也可以發現，如果一個提交沒有其他提交的父提交是它，則該分支可以被認為在該提交後死亡。

在分支的整個生命週期中，它應該被分配一個與所有活著的分支的顏色都不同的顏色。每當一個分支死去，原本該分支被分配的顏色可以再重新被分配給這之後新建立的分支。

現在，我們有了 Git 儲存庫的歷史。然而，我們只有提交的列表。對於每個提交，你會得到時間戳和父提交的索引。你的任務是確定需要多少種顏色來根據所述規則為圖表著色。