587 . RGB 檔處理器
TopCoder
Tags
Description
給定一個 $n\times m(1\le n,m\le 50)$ 的 RGB 圖檔，每格像素以三個 $0 \sim 255$ 的整數表示。請你實做一個功能將圖中某個指定顏色周圍曼哈頓距離小於等於 $d(1\le d\le 10)$ 的格子皆設為透明，並輸出一個 $n\times m$ 的 01 矩陣代表結果，1 代表透明，0 代表非透明。指定的顏色一樣以三個 $0 \sim 255$ 的整數表示（R、G、B）。
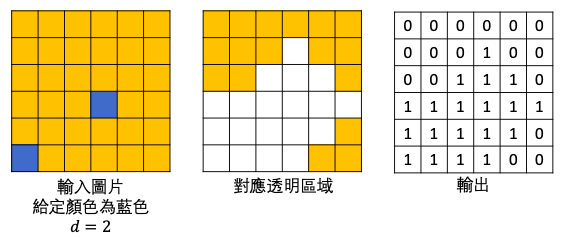
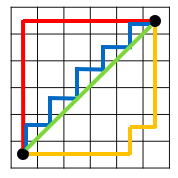
曼哈頓與歐幾里得距離： 曼哈頓距離的定義是只能水平和垂直移動時的最短距離。如圖，紅、藍與黃線皆為符合水平垂直條件的路徑，且都擁有一樣長度（$10$），因為這是所有方法中最短的所以曼哈頓距離為 $10$ ，而綠線則是歐幾里得距離的走法，長度為 $5\sqrt{2}\approx 7.07$ 。（截自維基百科）
Input Format
第一行有六個以單一空格分開的整數 $n,m,d,r_0,g_0,b_0$ 表示此圖檔的大小為 $n$ 列 $m$ 行，給定的曼哈頓距離為 $d$，指定的顏色為 $(r_0,g_0,b_0)$。
接下來的 $3n$ 行（line），每行有 $m$ 個 $0 \sim 255$ 的整數代表這個圖檔，前 $n$ 行每行代表 R 的值，再接著的 $n$ 行代表 G 值，最後 $n$ 行代表 B 值。
Output Format
輸出共有 $n$ 行，每行有 $m$ 個 0 或 1 的整數表示透明的情況。1 代表透明，0 代表非透明。
Sample Input 1
6 6 2 68 114 196 248 248 248 248 248 248 248 248 248 248 248 248 248 248 248 248 248 248 248 248 248 68 248 248 248 248 248 248 248 248 68 248 248 248 248 248 192 192 192 192 192 192 192 192 192 192 192 192 192 192 192 192 192 192 192 192 192 114 192 192 192 192 192 192 192 192 114 192 192 192 192 192 69 69 69 69 69 69 69 69 69 69 69 69 69 69 69 69 69 69 69 69 69 196 69 69 69 69 69 69 69 69 196 69 69 69 69 69
Sample Output 1
0 0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 0 0
Sample Input 2
5 5 2 121 240 174 236 210 215 14 108 69 247 61 228 219 206 208 196 129 222 54 1 135 121 4 146 37 137 113 244 39 120 253 175 5 175 107 45 18 201 134 149 36 228 136 85 56 31 240 159 236 32 27 234 3 53 202 52 125 153 162 79 168 38 193 158 79 242 140 105 120 217 8 174 141 248 99 169 219 49
Sample Output 2
0 0 0 0 0 0 0 0 1 0 0 0 1 1 1 0 1 1 1 1 0 0 1 1 1
Hints
Problem Source
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~1 | 範例測資 | 0 |
| 2 | 0~9 | 無額外限制 | 100 |