926 . 自我介紹
TopCoder
Tags
Description
全部台大資訊系的學生會加入一個社群軟體上的私密社團,每個被加入到社團的新生都會面臨到開學前的第一個挑戰:發自我介紹文(以下簡稱發自介)。然而,由於大家都生性害羞,大家只在認識的人發自介後 tag 到自己才會願意發自介。
假設台大資訊系總共有 $n$ 個人,每個人編號為 $1, 2, \ldots, n$,任兩個新生彼此互相認識的機率皆為 $\frac{p}{q}$ 且為獨立事件。假設每個人在發自介時都會 tag 所有他認識的人,請問在 $n$ 個人中有任一人率先發自介(此人不需先被 tag)後,最後 $n$ 人中有種馬沒發到自介的機率是多少?
Input Format
輸入第一行有三個整數 $n, p, q$,變數意義與題目敘述相同。
- $1\leq n\leq 4000$
- $1\leq p\leq q< 998244353, \gcd(p, q)=1$,其中 $\gcd(x, y)$ 表示 $x$ 和 $y$ 的最大公因數
Output Format
輸出一行。
如果答案是整數,請直接輸出。
否則,如果將答案以最簡分數表示為 $\frac{a}{b}$,請輸出唯一的 $r$ 滿足 $0 \leq r < 998244353$ 以及 $a \equiv b \times r \pmod{998244353}$。
換句話說,$r \equiv a \times b ^ {-1} \pmod{998244353}$,其中 $b ^ {-1}$ 為 $b$ 在模 $998244353$ 底下的乘法反元素,可以證明 $b$ 不為 $998244353$ 的倍數。
Sample Input 1
3 1 2
Sample Output 1
499122177
Sample Input 2
3 1 3
Sample Output 2
628524223
Sample Input 3
1 1 2
Sample Output 3
0
Sample Input 4
6 2025 48763
Sample Output 4
191593854
Hints
對於範例測資 $1$ 和 $2$,有人沒發到自介的可能情況如圖:
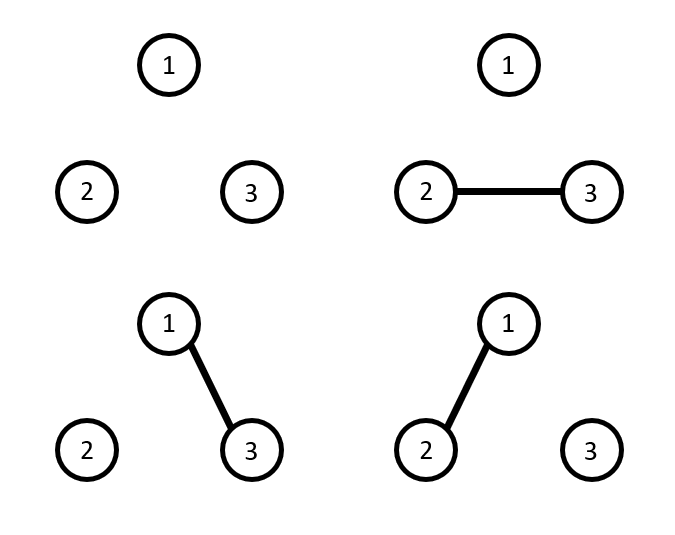
假設所有例子皆是由 $1$ 號種馬率先發自介:
- 左上圖:三人之間互不認識, $2, 3$ 號不會發到自介
- 右上圖:三人中僅 $2$ 號與 $3$ 號認識, $1$ 號並不認識 $2, 3$ 號,因此 $2, 3$ 號不會發到自介
- 左下圖:三人中僅 $1$ 號與 $3$ 號認識, $1, 3$ 號並不認識 $2$ 號,因此 $2$ 號不會發到自介
- 右下圖:三人中僅 $1$ 號與 $2$ 號認識, $1, 2$ 號並不認識 $3$ 號,因此 $3$ 號不會發到自介
對於範例測資 $1$,經過計算可知這些情況的發生機率總和為 $\frac{1}{2}$,因此答案為 $1\times 2 ^ {-1} \equiv 499122177 \pmod{998244353}$,
對於範例測資 $2$,經過計算可知這些情況的發生機率總和為 $\frac{20}{27}$,因此答案為 $20\times 27 ^ {-1} \equiv 628524223 \pmod{998244353}$。
可以證明由 $2$ 號種馬或 $3$ 號種馬先發自介時,其機率依舊相同。
Problem Source
IOICamp 2025 Day5 pC
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~3 | 範例測資 | 0 |
| 2 | 0~2, 4~53 | $n\leq 4$ | 1 |
| 3 | 0~66 | $n\leq 6$ | 4 |
| 4 | 0~93 | $n\leq 300$ | 25 |
| 5 | 0~109 | 無額外限制 | 70 |
