929 . 板子 2
TopCoder
Tags
Description
小波是個板子收藏家,他家裡有很多各式各樣的板子,像是有個板子上面寫著如何求出三維凸包、有個板子上面記載著如何以 $O(\lvert E \rvert \log \lvert V \rvert)$ 的時間複雜度找出有向最小生成樹。也有的板子充滿著神奇的魔法。
今天,他獲得了一個新的板子,這個板子可以視為一個左下角座標是 $(-10^ 9,-10^ 9)$、右上角是 $(10^ 9,10^ 9)$ 的平面正方形區域,在這個板子上有 $N$ 個特別的石頭,第 $i$ 個特別石頭的座標是 $(x_i,y_i)$。
小波很快就發現了這些石頭的特別之處:對於任兩顆不同石頭 $i,j$,都有一顆對它們而言的超特別石頭 $a_{i,j}$,$a_{i,j}$ 的決定方法是,對於所有不是 $i,j$ 的石頭 $k$,會使石頭 $i,j,k$ 為頂點的三角形面積不為 $0$ 而且最小的那一個就是 $a_{i,j}$,要是有很多這種 $k$ 的話,只有編號最小的那一個會是 $a_{i,j}$。當小波雙手摸著兩顆不同石頭 $i,j$ 時,$i,j,a_{i,j}$ 三顆石頭為頂點的三角形就會發光。
雖然小波玩了一下這個板子之後沒過多久就玩膩了,但他很好奇一個問題:令 $f(i,j)$ 是他摸著石頭 $i,j$ 時發光的三角形面積,$\sum\limits_{1 \leq i < j \leq N} 2f(i,j)$ 除以 $998244353$ 的餘數是多少?
Input Format
第一行有一個整數 $N$,代表板子上特別的石頭的數量。
接下來有 $N$ 行,其中第 $i$ 行有兩個整數 $x_i,y_i$,代表第 $i$ 顆特別的石頭座標是 $(x_i,y_i)$。
- $3 \leq N \leq 2000$
- $-10^ 9 \leq x_i,y_i \leq 10^ 9$
- 保證全部 $N$ 個石頭不在同一條直線上
- 任兩點不重合
Output Format
輸出一個整數,代表小波想要知道的數字。
Sample Input 1
5 2 2 10 4 6 3 6 6 3 4
Sample Output 1
75
Sample Input 2
5 2 2 10 4 7 1 6 6 3 4
Sample Output 2
111
Hints
$2f(i,j)$ 一定是正整數喔。
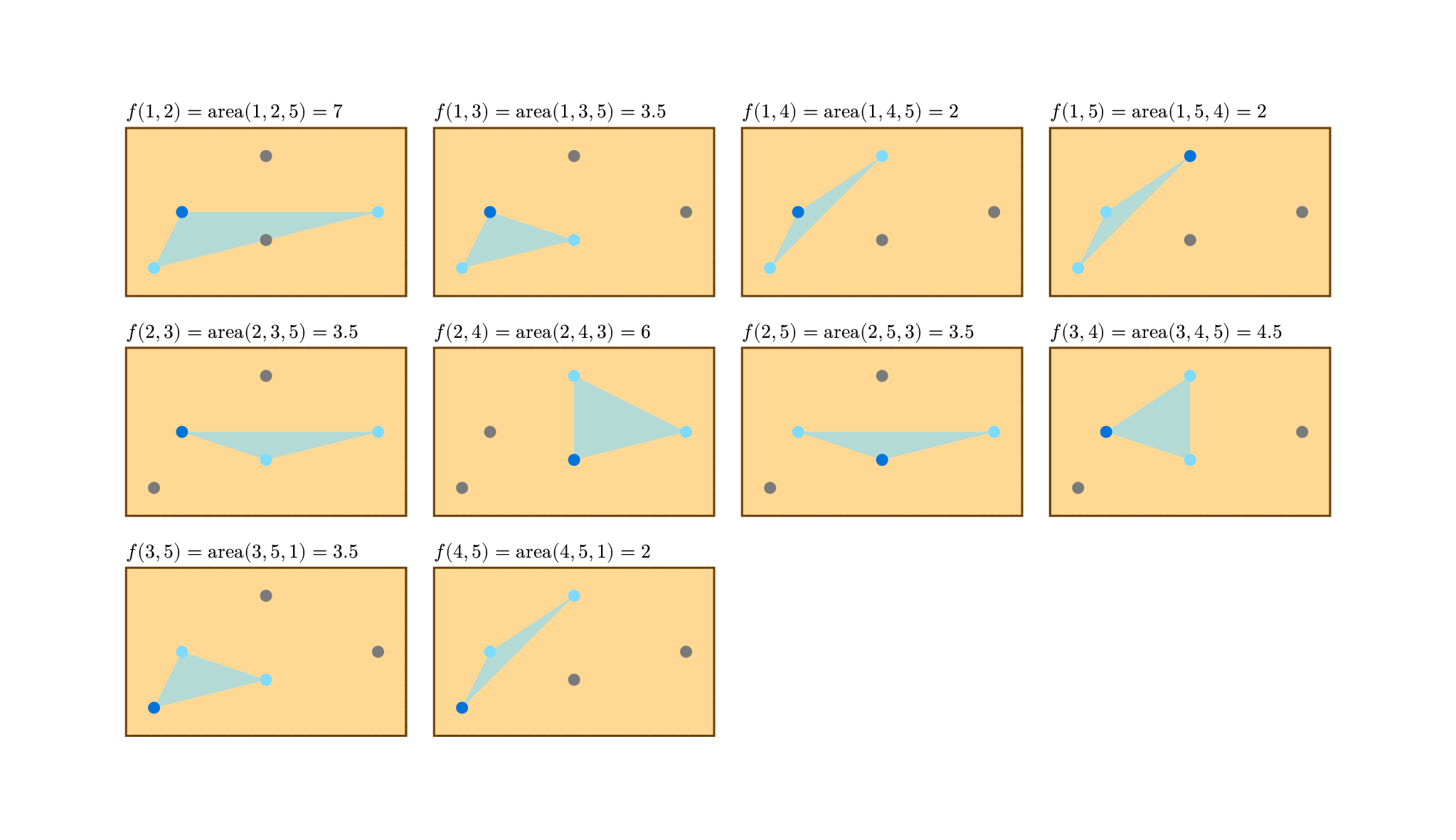
這是範例測資 1 中,小波摸著每一對石頭時,會發光的三角形。淺藍色點是小波摸著的兩顆石頭 $i,j$、深藍色點是 $a_{i,j}$。
Problem Source
IOICamp 2025 Day5 pF
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~1 | 範例測資 | 0 |
| 2 | 2~15 | $N \leq 500$ | 20 |
| 3 | 16~20 | 任三點不共線 | 50 |
| 4 | 0~33 | 無額外限制 | 30 |
