939 . PCC 和 Tetris
TopCoder
Tags
Description
在台灣某個大學中,有很多人喜歡打俄羅斯方塊遊戲 (Tetris),於是 PCC 決定要用俄羅斯方塊 (Tetris) 的積木設計一個遊戲,讓大家挑戰看看。
Tetris 的積木大小都是四格,形狀有 7 種,並且可以進行旋轉,但是不能翻轉:
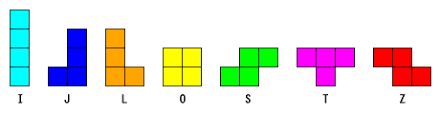

PCC 製作了一個大小為 $2 \times n$ 的木盒子,還有許多個 Tetris 積木,你的目標是要把 Tetris 積木全部都放到盒子裡。每一關 PCC 會給定每種積木需要用幾個,壞心眼的 PCC 有時候也會給你無法完成的關卡來欺騙你,如果可以的話你需要告訴 PCC 是怎麼擺放的,不行的話需要告訴 PCC 無法完成。
Input Format
第一行輸入一個正整數 $N$,代表盒子的長度。
第二行會輸入七個正整數,代表積木 I, J, L, O, S, T, Z 的數量。
由於 PCC 很奇怪,所以每個積木的數量都是奇數個。
- $1 \leq N \leq 10^ 5$
- $I + J + L + O + S + T + Z \leq 5 \times 10^ 4$
Output Format
如果無法擺放所有積木到盒子裡,輸出一行 "No" (不含引號)
如果可以擺放所有積木到盒子裡,輸出一行 "Yes" (不含引號)
接著輸出兩行,代表你怎麼把積木放進盒子的,擺放的方法如下:
- 使用整數為每個 tetris 方塊編號,同一個方塊佔據的所有格子必須使用相同的編號。
- 你可以自由選擇編號,只要從 1 開始,並依序遞增即可。
- 每一行的數字以空格隔開
- 可以參考範例測資的格式
Sample Input 1
21 1 1 1 1 1 1 1
Sample Output 1
Yes 1 1 2 3 3 3 3 4 0 5 5 6 7 7 0 0 0 0 0 0 0 1 1 2 2 2 4 4 4 5 5 6 6 6 7 7 0 0 0 0 0 0
Sample Input 2
4 1 1 1 1 1 1 1
Sample Output 2
No
Hints
第一個範例測資中,可以將全部的積木都放進盒子裡,因此輸出 Yes,並且把積木依序放入。
第二個範例測資中,無法將積木全部放入,因此輸出 No。
Problem Source
YTP 2025 高中組初賽 p3
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~1 | 範例測試資料 | 0 |
| 2 | 0~61 | 無額外限制 | 10 |
