949 . 魔法蛇神之儀式
TopCoder
Tags
Description
在遠古的奧爾托利亞大陸,傳說有一座名為「蛇神之塔」的神殿。
祭司們為了向蛇神祈雨,會舉行一種奇特的 「魔法蛇舞儀式」:
- 他們會用一串由 $n$ 段「靈蛇節」串接而成的魔法蛇,從地面蜿蜒向空中舞動。
- 每一段靈蛇節是由純能量凝聚而成,長度為 $L_i$。
- 每一段靈蛇節的相對轉角 $\theta_i$ 可以設定為 $0^ \circ, 90^ \circ, 180^ \circ, 270^ \circ$ 四種固定角度(因為這是蛇神咒文中允許的穩定魔法角度)。
- 靈蛇是從原點 $(0,0)$ 出發,初始沿著 $+\text{x}$ 軸方向延展。
- 每一段靈蛇節會先相對上一段旋轉逆時針 $\theta_i$,然後沿著當前方向平移 $L_i$ 長度。若為第一段靈蛇節,則直接從原點 $(0,0)$ 以 $\theta_1$ 角度($0^ \circ$ 為 $+\text{x}$ 軸,$90^ \circ$ 為 $+\text{y}$ 軸,$180^ \circ$ 為 $-\text{x}$ 軸,$270^ \circ$ 為 $-\text{y}$ 軸)出發,並平移 $L_1$ 長度。
在儀式進行過程中,祭司們可以不斷調整靈蛇節的轉角,或者查詢當前靈蛇在前 $k$ 段之後的末端位置,藉此判斷儀式進展是否成功。
一開始 $\theta_i$ 全部設為 $0^ \circ$。儀式過程中有 $q$ 次操作,分為以下三種:
觀測靈蛇
1 k— 查詢前 $k$ 段靈蛇節合成之後的末端位置 $(x, y)$。變更咒文(改變角度)
2 x theta— 將第 $x$ 段靈蛇節的轉角設為 $\text{theta}^ \circ$,其中 $\text{theta} \in \lbrace 0, 90, 180, 270\rbrace$。變更咒文(改變長度)
3 x len— 將第 $x$ 段靈蛇節的長度改為 $\text{len}$,其中 $\text{len}$ 為正整數。
換句話說,你需要計算從原點出發,按照前 $k$ 段當前設定的旋轉和平移,最終位置會到哪裡。
Input Format
輸入的第一行包含兩個正整數 $n$、$q$,代表靈蛇節的數量和操作的次數。
第二行包含 $n$ 個正整數 $L_1, L_2, \ldots, L_n$,代表每段靈蛇節的長度。
接下來的 $q$ 行,每行包含一個操作,格式如下:
1 k:查詢前 $k$ 段靈蛇節合成之後的末端位置。2 x theta:將第 $x$ 段靈蛇節的轉角改為 $\text{theta}^ \circ$,其中 $\text{theta} \in \lbrace 0, 90, 180, 270\rbrace$ 且 $1 \leq x \leq n$。3 x len:將第 $x$ 段靈蛇節的長度改為 $len$,其中 $1 \leq \text{len} \leq 10^ 9$ 且 $1 \leq x \leq n$。
資料範圍:
- $1 \leq n, q \leq 2 \times 10^ 5$。
- $1 \leq L_i \leq 10^ 9$ ($1 \leq i \leq n$)。
- 對於每個操作:
1 k,其中 $1 \leq k \leq n$。2 x theta,其中 $\text{theta} \in \lbrace 0, 90, 180, 270\rbrace$。3 x len,其中 $1 \leq \text{len} \leq 10^ 9$。
Output Format
對於每個查詢操作 1 k,輸出一行,包含兩個整數 $x$ 和 $y$,代表前 $k$ 段靈蛇節合成之後的末端位置 $(x, y)$。
Sample Input 1
3 5 1 2 8 1 3 2 3 180 1 3 3 2 1 1 3
Sample Output 1
11 0 -5 0 -6 0
Sample Input 2
4 5 2 3 1 4 1 4 2 2 90 3 1 1 3 2 1 1 4
Sample Output 2
10 0 1 6
Sample Input 3
4 6 1 1 1 1 1 4 2 1 90 2 3 90 2 2 90 2 4 90 1 4
Sample Output 3
4 0 0 0
Hints
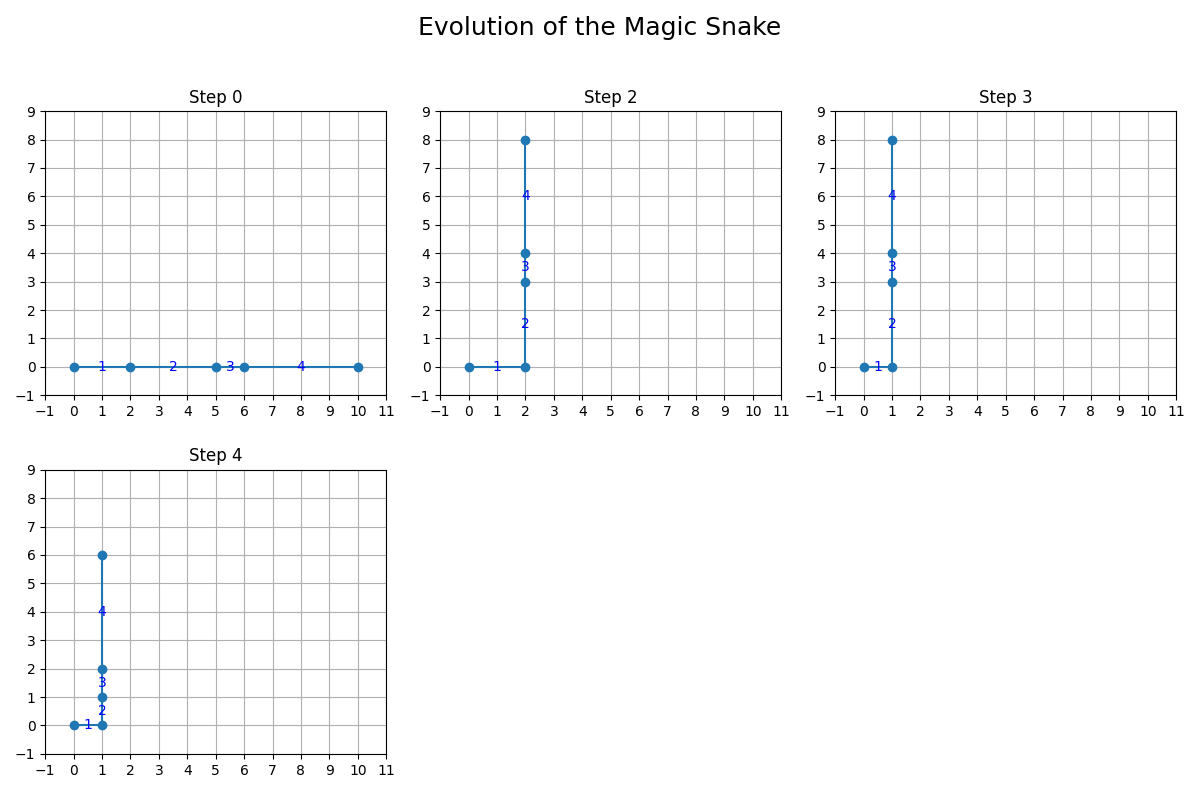
範例 1 的每一步操作後的結果如下圖所示:

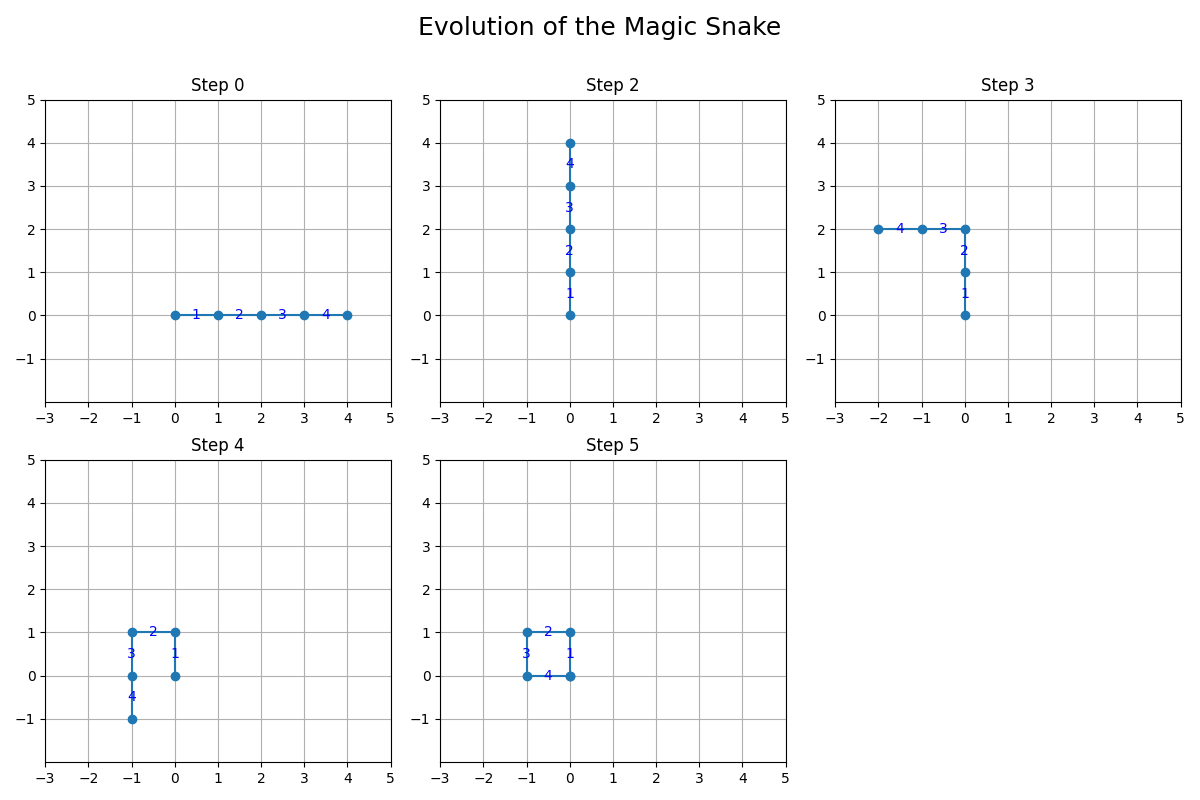
範例 2 的每一步操作後的結果如下圖所示:
範例 3 的每一步操作後的結果如下圖所示:
Problem Source
YTP 2025 國中組初賽 p5
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~2 | 範例測試資料 | 0 |
| 2 | 0~12 | $1 \leq n, q \leq 2 \times 10^ 3$ | 4 |
| 3 | 13~22 | 對於每個指令 2 x theta 的 $\text{theta} \in \lbrace 0, 180\rbrace$ |
8 |
| 4 | 0~32 | 無額外限制 | 8 |
