951 . 芒果大進擊
TopCoder
Tags
Description
芒果喜歡到處跟人玩遊戲,像是西洋棋、圍棋、Nim、Hackenbush 等等的雙人遊戲,他都很喜歡。最近,他最喜歡的遊戲是剪刀石頭布,剪刀石頭布的玩法是兩名玩家要同時比出剪刀、石頭、布的其中一種手勢,如果兩人比出的手勢一樣,那遊戲結果就是平手,否則按照下圖決定勝負:
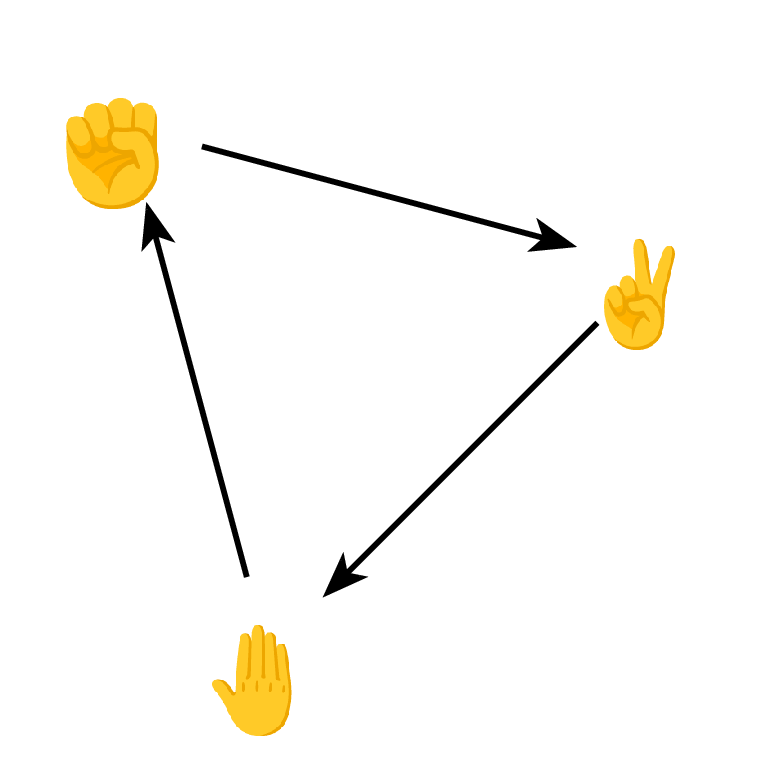
這張圖裡面,$A \to B$ 代表手勢 $A$ 會打贏 $B$。舉例來說,如果一個玩家出了剪刀、另一個出了布,那就會由出剪刀的那名玩家獲得勝利。
聰明的芒果覺得這個遊戲只有三種手勢,實在是太無趣了!於是他發明了一個新的遊戲,叫作芒果大進擊,芒果大進擊有 $N$ 種手勢,$N$ 是一個奇數,這些手勢從 $1$ 到 $N$ 編號。跟剪刀石頭布差不多,兩個玩家要同時比出 $N$ 個手勢的其中一種,一樣的話就是平手,否則就根據兩人出的手勢之間的勝負關係決定勝負。為了公平,每一種手勢都剛好贏過 $\lfloor N/2 \rfloor$ 個手勢、輸給 $\lfloor N/2 \rfloor$ 個手勢,為了決定每個手勢之間的勝負關係,想像手勢 $1,2,\dots,N$ 按照順時針順序排成一圈,每個手勢都會贏過它順時針方向最近的 $\lfloor N/2 \rfloor$ 個手勢、輸給逆時針方向最近的 $\lfloor N/2 \rfloor$ 個手勢。
發明了芒果大進擊之後,芒果覺得這個遊戲真是太棒了,於是到處找人陪他一起玩。然而,不是每個人都可以記得住全部 $N$ 個手勢怎麼比,芒果在跟許多朋友玩過這個遊戲之後,發現每個人都只記得住其中三種手勢而已。芒果告訴你他每個朋友記住的三個手勢是什麼,請你幫他找出一種手勢,使得不管對方出他記住的三個手勢的哪一種,芒果只要出這個手勢就一定會贏,或是告訴他這個朋友很聰明,不存在必定會讓他贏的手勢。
下圖是一個 $N=9$ 時的例子,假設有個朋友只會出手勢 $6,7,8$,那麼芒果只要出手勢 $4$ 就一定會贏。
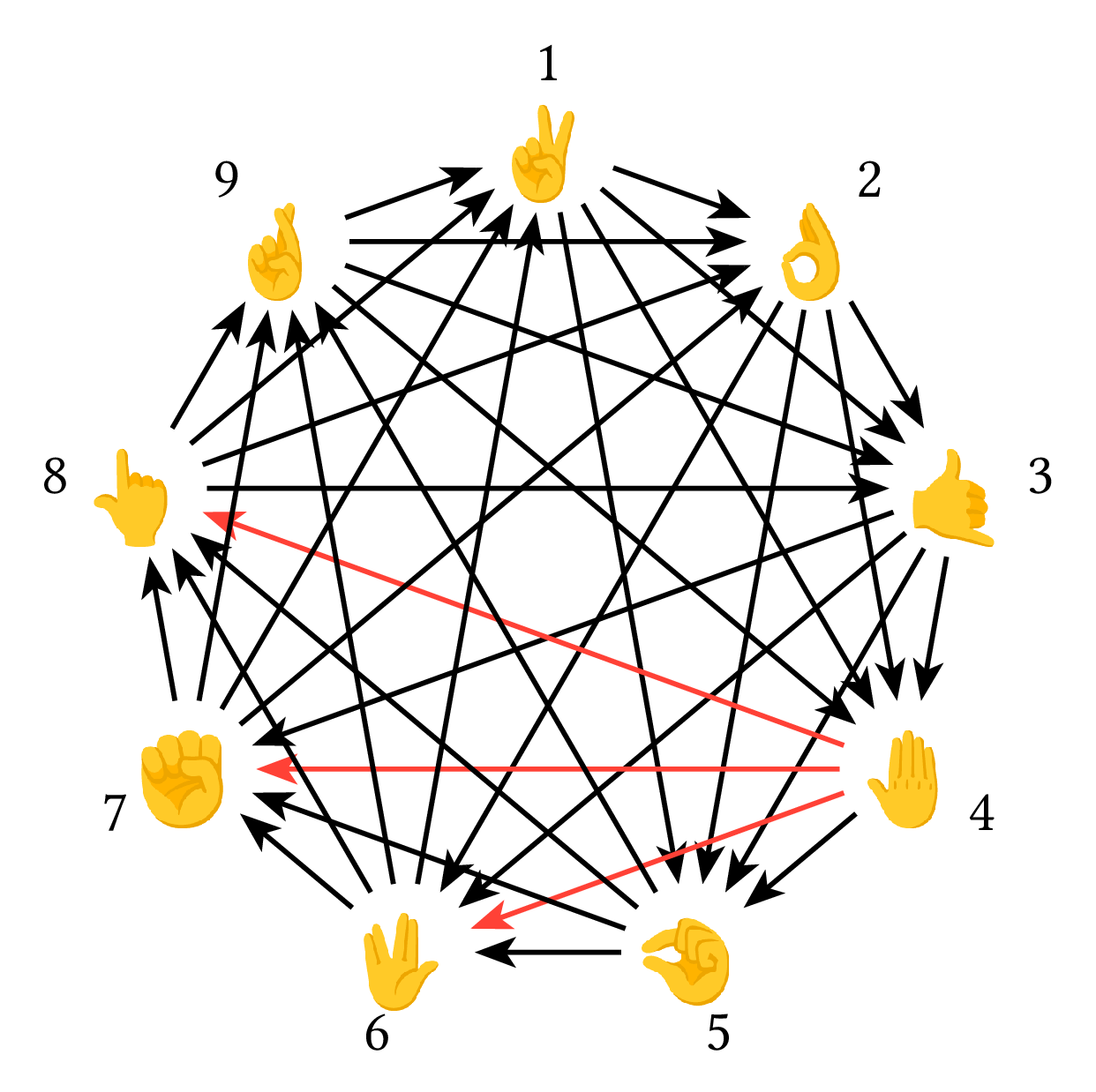
注意平手不算是贏。
Input Format
第一行有兩個整數 $N,Q$,代表芒果大進擊裡有幾種手勢,以及芒果有幾個會跟他玩芒果大進擊的朋友。
接下來有 $Q$ 行,其中第 $i$ 行有三個整數 $x_i,y_i,z_i$,代表第 $i$ 個朋友記住的三種手勢。
- $3 \leq N \leq 10^ 3$
- $N$ 是奇數
- $1 \leq Q \leq 10^ 3$
- $1 \leq x_i,y_i,z_i \leq N$
- $x_i \neq y_i,\ y_i \neq z_i,\ x_i \neq z_i$
Output Format
輸出 $Q$ 行,其中第 $i$ 行包含一個整數 $s_i$,代表只要芒果出手勢 $s_i$,就一定會贏第 $i$ 個朋友。如果有多種必勝手勢,輸出編號最小的。如果不存在必勝手勢,輸出 -1。
Sample Input 1
9 6 4 5 6 6 9 1 7 6 4 7 1 9 2 1 9 8 3 1
Sample Output 1
2 -1 3 6 7 -1
Hints
Problem Source
YTP 2025 高中組程式挑戰營 p1
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0 | 範例測試資料 | 0 |
| 2 | 0~8 | 無額外限制 | 5 |
