955 . 構造 DAG
TopCoder
Tags
Description
給定一張有 $n$ 個點、$m$ 條邊的無向圖 $G = (V, E)$。
現在給定根節點的位置 $r$,以及每個節點 $v \in V$ 所需的入度 $d_v$,請你將 $G$ 中的每條邊指定方向,使得圖變成一張有向無環圖(DAG),並滿足以下條件:
- 圖中有且僅有一個指定的根節點 $r$。
- 每個節點 $v$ 的入度正好是 $d_v$。
在 DAG 中,根節點是指一個節點,從它出發可以沿著有向邊到達圖中所有其他節點。
Input Format
輸入的第一行包含三個整數 $n, m$ 和 $r$,分別代表節點數、邊數,以及根節點的編號。
第二行包含 $n$ 個整數 $d_1, d_2, \dots, d_n$,其中 $d_i$ 表示節點 $i$ 的目標入度。
接下來的 $m$ 行中,每行包含兩個整數 $u_i$ 和 $v_i$,表示在節點 $u_i$ 和 $v_i$ 之間存在一條無向邊。
所有節點的編號皆為 1-based(從 1 開始)。
- $1 \leq n \leq 10^ 5$
- $1 \leq m \leq 2 \times 10^ 5$
- $1 \leq r \leq n$
- 對於所有 $1 \leq i \leq n$,皆有 $0 \leq d_i \leq m$
- 對於所有 $1 \leq i \leq m$,皆有 $1 \leq u_i, v_i \leq n$ 且 $u_i \ne v_i$
- 給定的圖 $G$ 為一張簡單圖(無自環且無重邊),且為連通圖。
Output Format
如果不存在任何合法的邊方向指定方式,請輸出 "NO"(不含引號)。
如果存在多種合法的邊方向指定方式,請輸出 "MULTIPLE"(不含引號)。
如果僅有唯一一種合法的邊方向指定方式,請輸出 "YES"(不含引號),接著輸出 $m$ 行。
每行包含兩個整數 $u$ 和 $v$,表示對應的無向邊被定向為從節點 $u$ 指向節點 $v$ 的有向邊。
輸出的邊的順序必須與輸入中的邊的順序完全一致。
Sample Input 1
4 6 1 0 1 3 2 1 2 4 2 1 3 3 2 4 1 3 4
Sample Output 1
YES 1 2 2 4 1 3 2 3 1 4 4 3
Sample Input 2
5 7 4 3 2 1 0 1 5 4 4 3 3 2 1 5 1 3 2 1 2 4
Sample Output 2
YES 4 5 4 3 3 2 5 1 3 1 2 1 4 2
Hints
範例 1
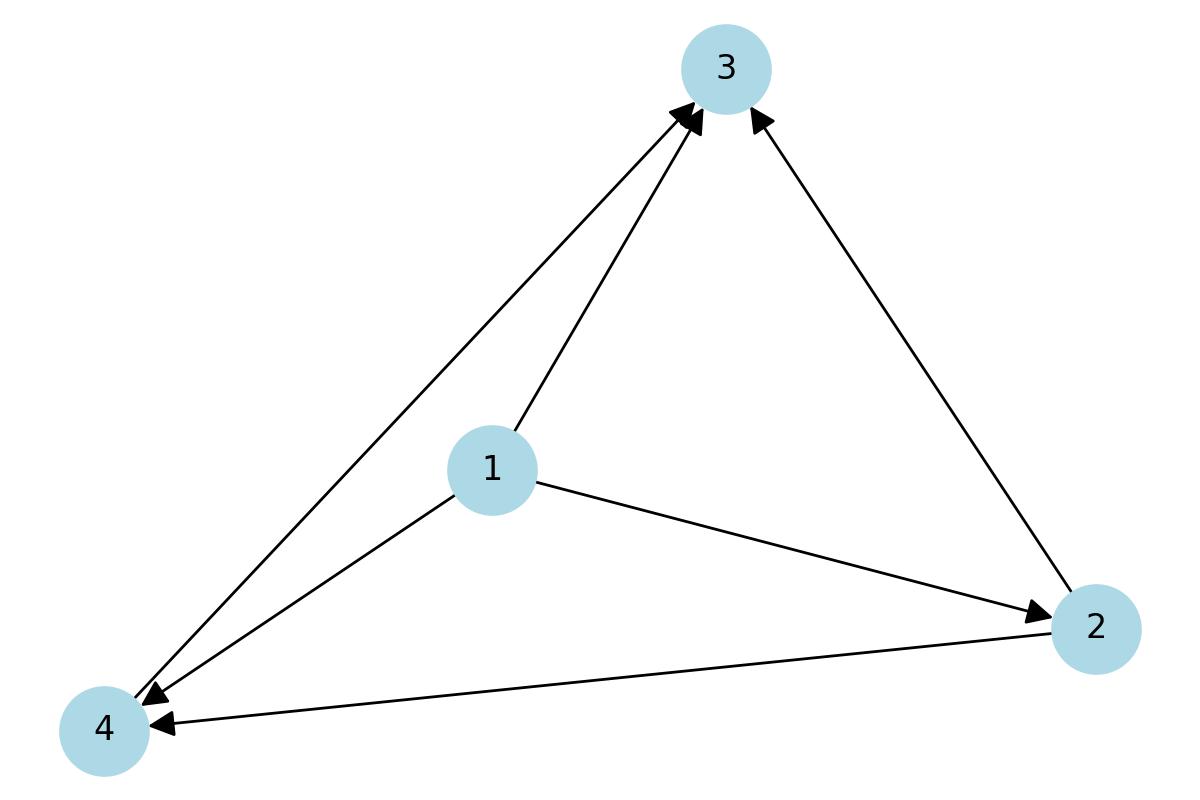
輸出的邊方向指定方式滿足所有條件:
- 節點 1 為根節點(入度為 0),且圖中所有其他節點皆可由此到達。
- 各節點的入度如下:
- 節點 1:0
- 節點 2:1
- 節點 3:3
- 節點 4:2
- 該圖為無環,且所有入度需求皆符合。
- 輸出中的每條邊皆按照輸入中的順序給出。
範例 2
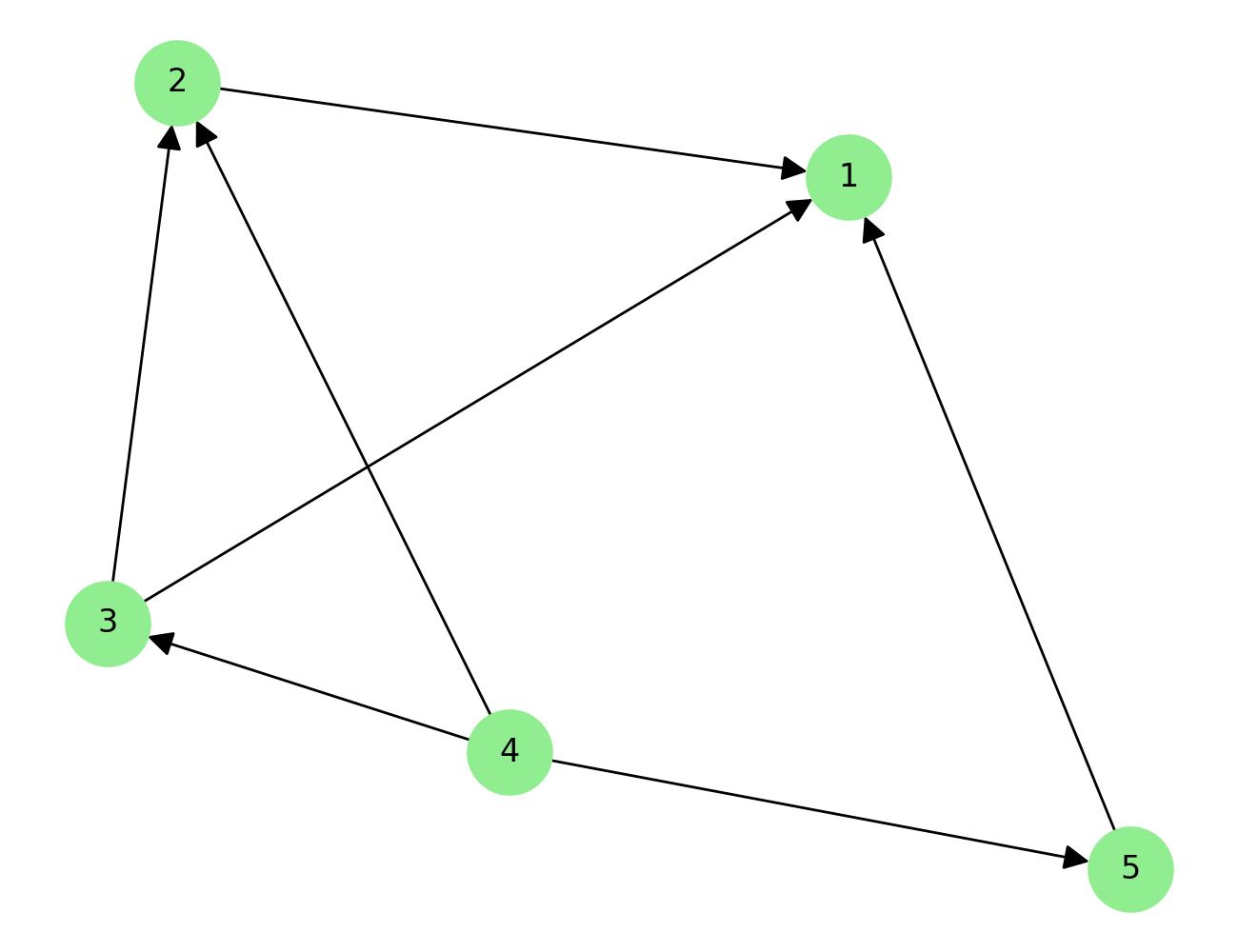
輸出的邊方向指定方式滿足所有條件:
- 節點 4 為根節點(入度為 0),且圖中所有其他節點皆可由此到達。
- 各節點的入度如下:
- 節點 1:3
- 節點 2:2
- 節點 3:1
- 節點 4:0
- 節點 5:1
- 該圖為無環,且所有入度需求皆符合。
- 輸出中的每條邊皆按照輸入中的順序給出。
Problem Source
YTP 2025 高中組程式挑戰營 p5
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~1 | 範例測試資料 | 0 |
| 2 | 0~5 | $n, m\leq 20$ 且保證有唯一一組解 | 2 |
| 3 | 0~11 | 保證有唯一一組解 | 5 |
| 4 | 0~24 | 無額外限制 | 8 |
