957 . 梯子
TopCoder
Tags
Description
來自「楓之島」的精靈,也就是你,誤入了位於「玩具城」的「時間通道」。用盡回家卷軸的你,必須獨自攀爬數千階的梯子。
在你爬到恍神之時,你突然想起家鄉「魔法森林」,那裡的樹木高大挺拔,陽光透過樹葉灑下斑駁的光影,讓你感到一陣思念之情湧上心頭。
無聊的你不禁好奇,在這座梯子中,究竟能找到多少棵樹。
具體來說,$n$ 階的梯子可以被視為一張圖,包含 $2n$ 個點與 $3n - 2$ 條邊。對於每個 $1 \le i \le n$,圖中會有一條邊連接 $i$ 與 $n+i$;對於每個 $1 \le j < n$,圖中會有兩條邊,分別連接 $j$ 與 $j+1$,以及 $n+j$ 與 $n+j+1$。
更具體的例子可以參考下方圖片:
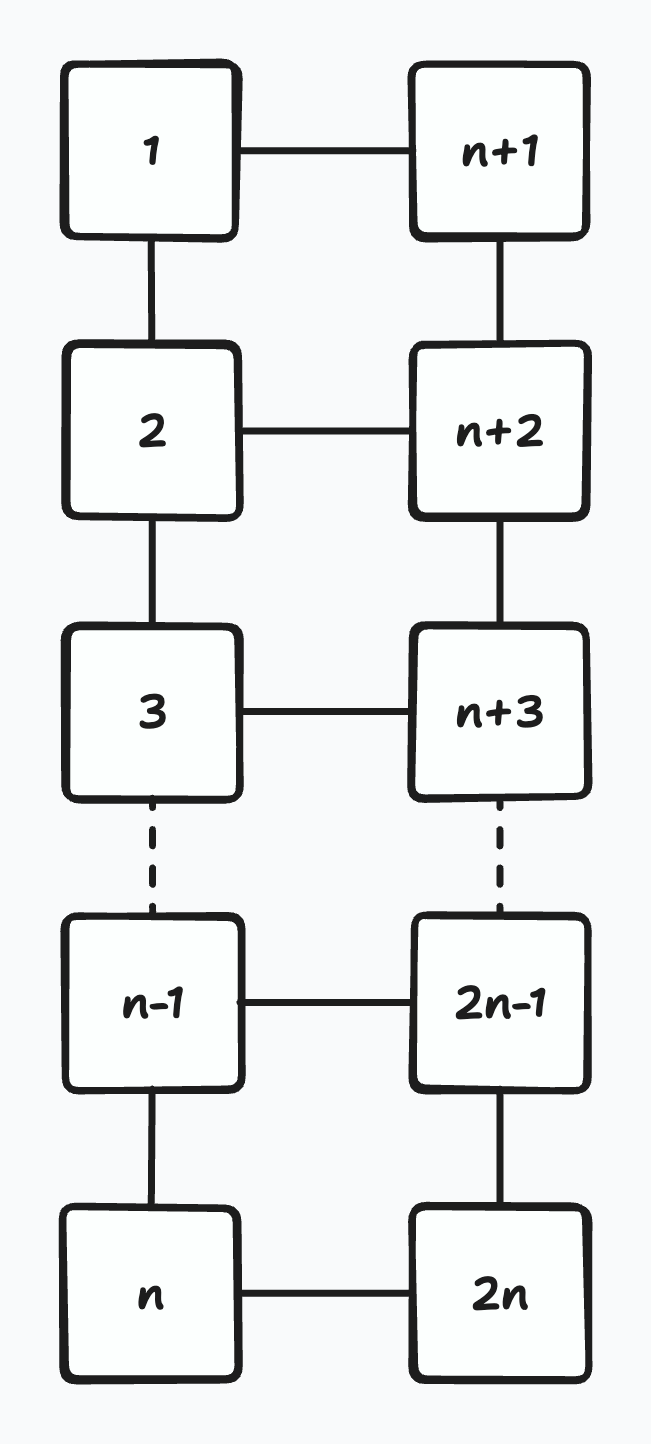
一棵樹可以被梯子「找到」,指的是你可以從圖中選出一個大小為 $2n - 1$ 的邊集,使得圖中所有的點皆為連通的,且不含任何環。
若兩個邊集 $E_1$、$E_2$ 不相同,則視為兩棵不同的樹。請你計算,在這張圖中總共可以找到多少棵不同的樹。
Input Format
輸入有一行,包含一個正整數 $n$,代表梯子的階數。
- $1 \leq n \leq 10^ {18}$
Output Format
輸出一個正整數,代表代表有多少顆樹可以在 $n$ 階的梯子內找到。
由於數字可能很大,請輸出除以 $10^ 9 + 7$ 的餘數。
Sample Input 1
5
Sample Output 1
209
Sample Input 2
50
Sample Output 2
656096480
Hints
Problem Source
YTP 2025 高中組程式挑戰營 p7
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~1 | 範例測試資料 | 0 |
| 2 | 0~9 | $1 \le n \le 5 \times 10^ 5$ | 12 |
| 3 | 0~19 | 無額外限制 | 3 |
