958 . 小茂與小盛
TopCoder
Tags
Description
小茂和小盛是自兒少時期就相當要好的夥伴,他們一起上下學、一起參加人生中大大小小的考試、一起進入理想的科系、一起追求改變世界的夢想。
秋天到了,小茂小盛倆來到了一片森林,這片森林似乎是為了抵禦全球暖化而人工規劃種植的,所有的樹整齊的排列在數條平行的直線上,或許對於某些人來說這樣的景色實在是詭異的整齊,或甚至懷疑是 AI 生成的場景,但在小茂和小盛兩位的眼裡可不是如此,他們心裡想的是,從高處俯瞰空拍看起來會是多麼壯觀的樣貌。
這片森林總共有 $n$ 條種滿樹木的線段,每條線段都與 $y$ 軸平行,第 $i$ 條線段可以以 $x$ 座標 $x_i$ 以及 $y$ 座標區間 $[y_{\min, i}, y_{\max, i}]$ 表示,這些線段彼此不會相交。小茂小盛的帳篷在原點(座標 $(0, 0)$)上,為了保留兩側寬敞的視野,他們的帳篷位置不會與任何一個樹木的線段有相同的 $x$ 座標。他們想要拍一張壯闊的空拍照片紀錄這個時刻,他們希望經過旋轉與移動鏡頭後,這張照片要包含這片森林的所有樹木,他們的帳篷也要在這張照片的垂直中線上,稍微試拍幾張照片之後,他們總是對這些結果有一點不滿意。稍微思考一陣之後,他們意識他們少了一個最重要的性質,「平分秋色」:照片中線的兩邊樹木線段的總長度應該要一樣長。
以範例一為例,下圖 (a) 中,小茂小盛的帳篷所在位置由黑點所示,而樹木線段則為綠色的鉛直線段。如果以圖 (b) 的方式拍攝照片,也就是照片的垂直中線是通過 $(0, 0)$ 以及 $(0, 1)$ 的直線,左右兩側的樹木線段的總長度分別是 $4$ 與 $3$,沒有達到他們的目標。若是旋轉鏡頭使得照片的垂直中線通過 $(0, 0)$ 以及 $(-0.4, 1)$ 的直線,如圖 (c) 所示,那左右兩側的樹木線段的總長度就會都是 $3.5$,滿足小茂小盛心目中的所有條件。
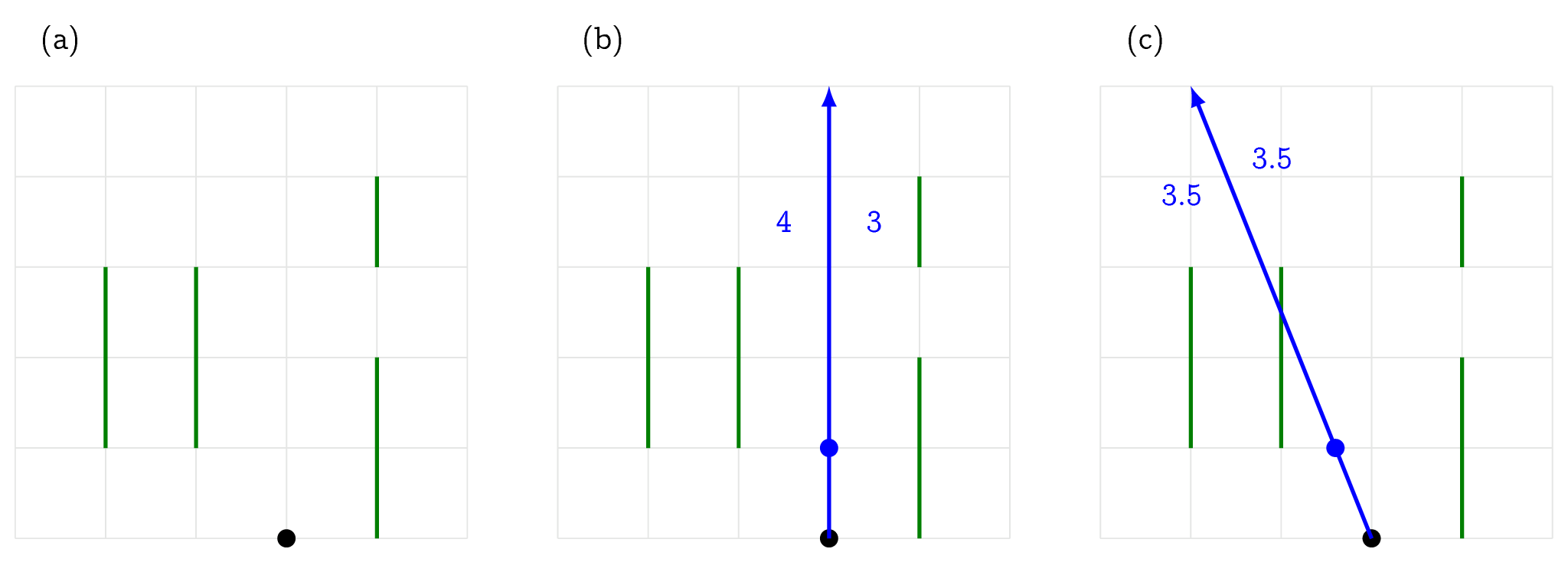
小茂小盛倆看著這些失敗的嘗試,思考這條完美的中線,看著彼此扭曲的神情,忍不住笑了出來。然而,或許就是這聲笑放鬆了他們倆的思考路線,打開了通往完美解答的道路,一陣解開問題的滿足瞬間湧上他們的心頭,解決了平分樹木線段景色的問題,就是所謂的「笑能平景」。
你能找到這條中線,一起體會解開問題的滿足感嗎?
Input Format
輸入的第一行只有一個整數 $n$,代表樹木線段的數量。接著有 $n$ 行,第 $i$ 行有三個以空白分開的整數 $x_i, y_{\min, i}, y_{\max, i}$,代表第 $i$ 條樹木線段的座標範圍。
- $1 \leq n \leq 3 \times 10^ 5$
- $|x_i|, |y_{\min, i}|, |y_{\max, i}| \leq 10^ 6$
- 對於所有 $i$,$x_i \neq 0$。
- 對於所有 $i$,$y_{\min, i} < y_{\max, i}$。
- 任意兩條相異線段不相交。
Output Format
輸出兩個以空白分開的實數 $x, y$ 代表第二個在相片中線上點的座標 $(x, y)$。為了避免浮點數計算的誤差,你的輸出必須滿足以下三個條件才會被視為正確:
- $x^ 2 + y^ 2 \geq 1$。
- $|x|, |y| \leq 10^ {12}$。
- 在中線兩側的樹木線段長度差不超過 $n \cdot 10^ {-4}$。
可以證明在題目的設定下總是有至少一組正確答案。
Sample Input 1
4 1 0 2 1 3 4 -1 1 3 -2 1 3
Sample Output 1
-0.4 1
Sample Input 2
5 1 2 3 2 -3 -1 -1 -3 2 -2 1 3 -2 -2 0
Sample Output 2
1 0.333333
Sample Input 3
6 1 0 1 2 -1 0 3 0 1 4 -1 0 5 0 1 6 -1 0
Sample Output 3
1 0
Hints
在第二與第三個範例中,範例輸出的相片中線如下圖所示。
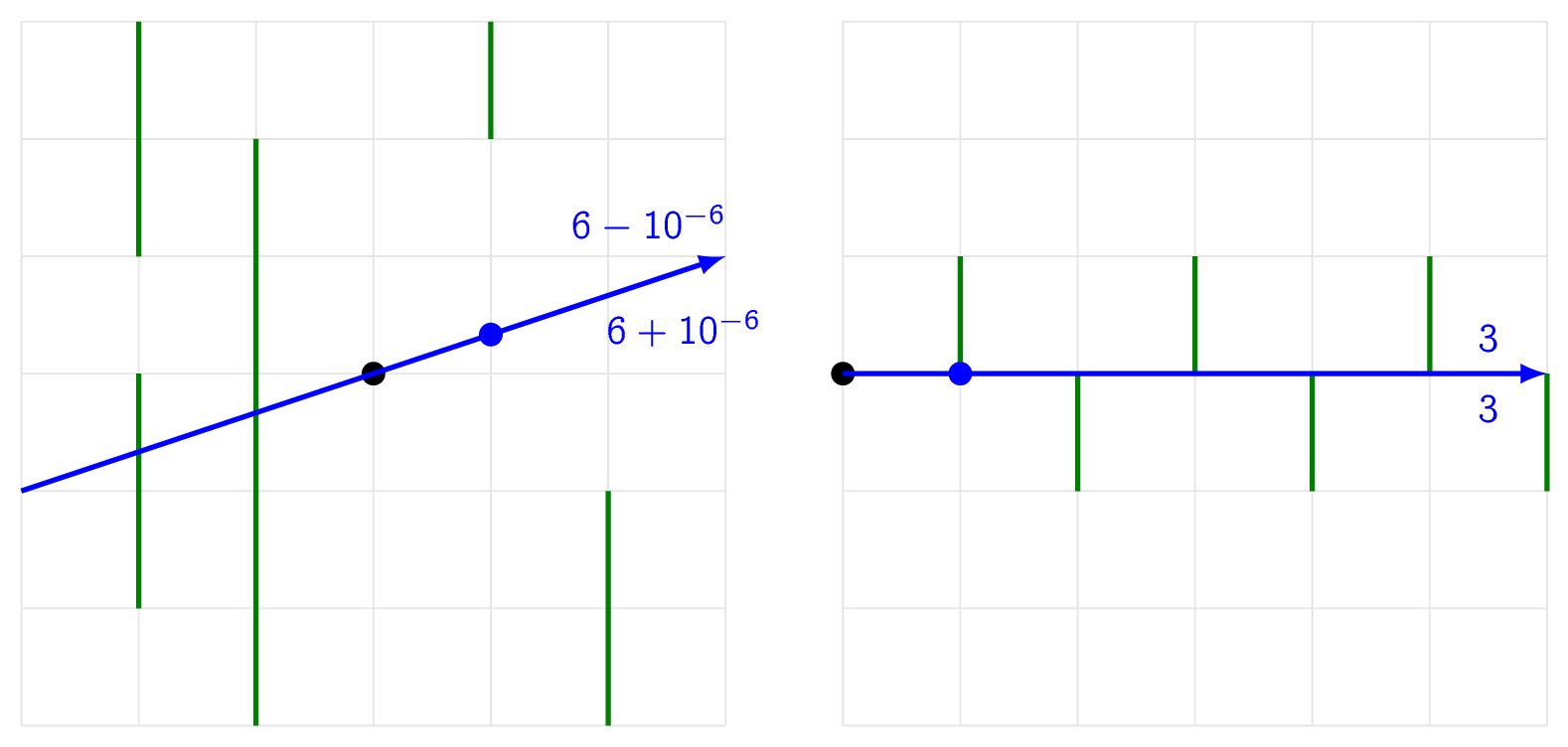
Problem Source
YTP 2025 高中組程式挑戰營 p8
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~2 | 範例測試資料 | 0 |
| 2 | 0~24 | 無額外限制 | 15 |
