964 . 蛇頭燙傷了
TopCoder
Tags
Description
splix.io 是一款基於區域控制概念的即時多人線上遊戲。玩家操控一條代表自身勢力的蛇,在由方格構成的地圖上移動並佔領區域。每當玩家離開自己的領地,蛇的移動路徑上會留下痕跡。若成功繞行並回到領地,所包圍的區域將歸入自己的版圖。玩家需謹慎規劃路徑,避免與自身或他人的痕跡相撞,同時尋找機會攻擊對手。遊戲兼具戰略性與風險管理,最終排名依據玩家佔領的面積決定。
在本題中,考慮一個不同的情境:棋盤上只有你控制的蛇,並且可能存在若干「燒紅的石頭」。蛇的移動遵循以下規則:
- 蛇初始位於格子 $S$,該格視為其起始領地。
- 每次移動,玩家可選擇將蛇頭朝向上、下、左或右中的其中一個方向,並向前移動一格。蛇不可移出棋盤邊界。
- 蛇離開領地時,移動途中會在經過的格子上留下痕跡,稱為其「身體」。
- 若蛇頭在移動過程中碰觸到自己的身體,則會被視為死亡。
- 若蛇成功返回任一己方領地格,則路徑所形成的封閉區域(注意與原本遊戲的判定有些許不同,下點說明)的所有格子將被視為成功佔領,並成為新的領地,同時所有產生的身體會全部消失並轉換成新的領地。
- 佔領事件發生時,定義邊 $X$ 為從回到領地時頭的格子與前一個時刻的格子中間的邊,邊 $Y$ 為第一次離開領土的格子與離開領土前的格子中間的邊,從 $X$ 向左(前述定義的前方逆時針轉 90 度)沿著領地邊緣(領土與空地的交界處)延伸直到 $Y$,由 $Y$ 沿著身體的右側延伸回 $X$,所形成的封閉路徑稱為封閉區域。
- 若佔領的區域包含任一顆燒紅的石頭,亦視為死亡。
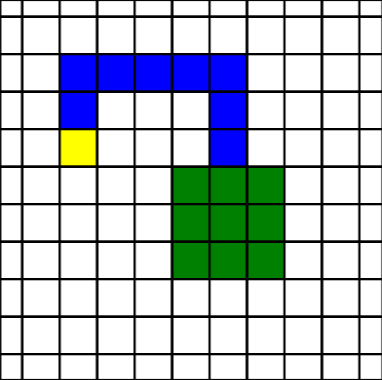
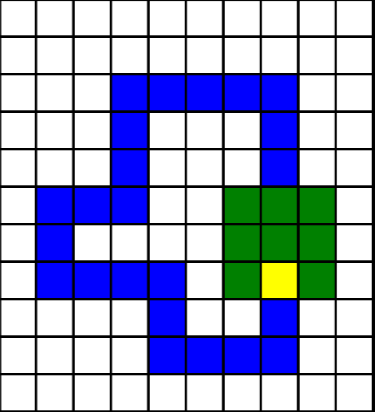
以下是遊玩畫面的示例。圖中綠色區域是領地,藍色部分是蛇的身體,黃色部分是蛇的頭部。下一回合若要避免撞到身體,蛇只能選擇向左、右或向下移動。
碰到身體的情況如下:
| 碰到身體前 | 碰到身體後 |
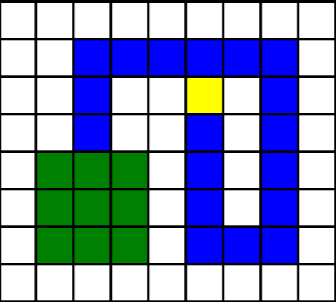 | 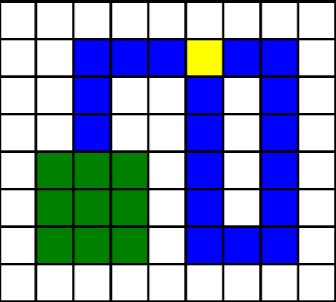 |
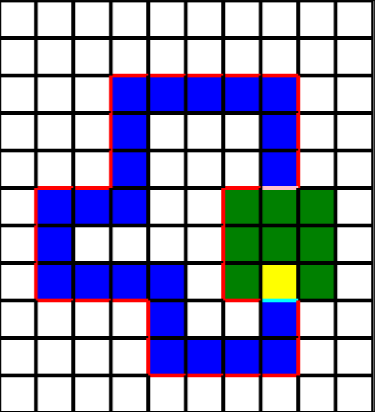
以下是佔領領地的過程。淺藍色的是 $X$ 邊,粉紅色的是 $Y$ 邊,紅色內部為封閉區域。
| 佔領領地前 | 正在佔領 | 計算封閉區域 | 佔領領地後 |
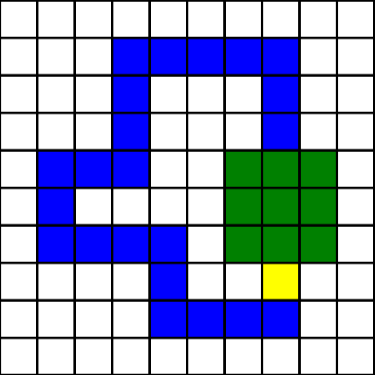 |  |  |  |
包圍燒紅的石頭也是不被允許的行為,下圖中紅色的格子代表燒紅的石頭。
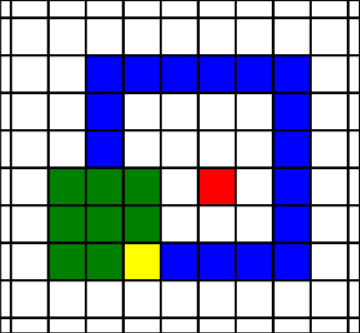
現在,給定一個 $N \times M$ 的棋盤,初始位置在 $S$,並存在若干燒紅的石頭。在可以無次數上限移動且不死亡的前提下,試問蛇所能成功佔領的最大格子數是多少。
Input Format
第一行輸入有兩個數字 $N, M$,分別代表棋盤的長和寬。
接著 $N$ 行每行有 $M$ 個字母,分別表示棋盤上每個格子上面有什麼。其中:
-
S表示蛇的初始位置 #表示燒紅的石頭.表示空白
資料範圍:
- $1 \leq N \times M \leq 10^ 6$
Output Format
輸出一個正整數,代表可以佔領的最大格子數。
Sample Input 1
3 3 ... S#. ...
Sample Output 1
1
Sample Input 2
3 3 ..# S.. #..
Sample Output 2
7
Sample Input 3
3 3 ... S.. #.#
Sample Output 3
6
Sample Input 4
5 5 #...# ..... S.#.. ..... #...#
Sample Output 4
20
Sample Input 5
7 7 ....... ....... ...#... ..###.. #...... ##..... ##....S
Sample Output 5
39
Hints
小提醒:移動方向可能會影響封閉區域的判定。
| 範例的方向 | 反著走 |
 | 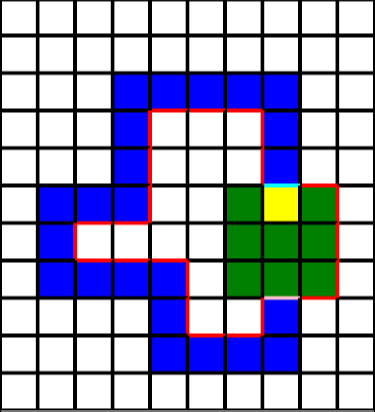 |
Problem Source
YTP 2025 高中組程式挑戰營 p14
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~4 | 範例測試資料 | 0 |
| 2 | 0~23 | 無額外限制 | 20 |
