969 . 三角剖分
TopCoder
Tags
Description
三角初華在地下室修建了一個多邊形造景,豊川祥子看到之後給初華出了一道難題。
你知道 Polygon 嗎?他是一個可以用來生測資的網站。
但這題不是在說那個 Polygon,是數學上的 polygon。
不用擔心,這並不是一道幾何題。題目如下:
有 $n$ 個點依序排在正 $n$ 邊形的頂點上,編號 $0, 1, \ldots, n-1$,且一開始在所有 $i$ 跟 $(i+1) \bmod n$ 之間都有一條邊(筆直的線段)。
舉例來說,當 $n = 6$ 時,初始狀態如下所示:
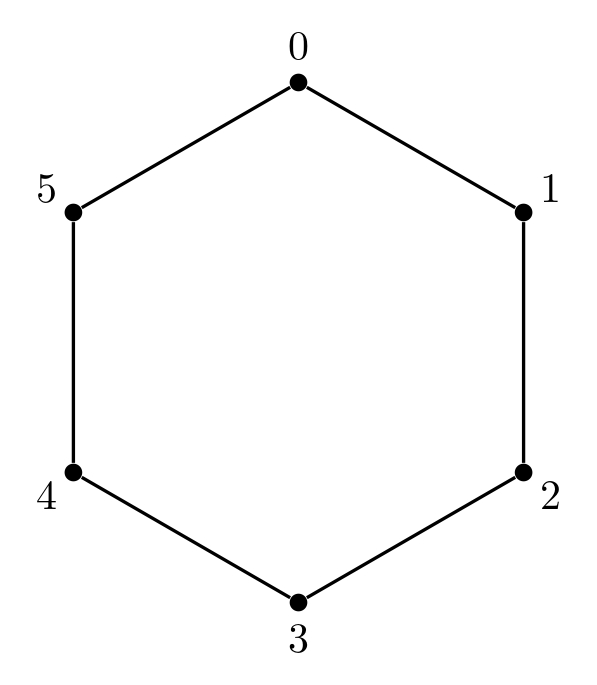
接著有 $n-3$ 次的操作,每次祥子會選一個點對 $(u_i, v_i)$ 並畫一條筆直的線段經過點 $u$ 跟點 $v$,保證這條線段跟之前所有線段皆不會交叉(可以相交於端點)。
請輸出 $n-2$ 個非負整數 $q_0, q_1, \ldots, q_{n-3}$,$q_i$ 代表在第 $i$ 次操作之後這張圖的生成樹數量 $\bmod 998\,244\,353$。
Input Format
- line $1$: $\;\; n$
- line $1+i$ ($1 \le i \le n-3$): $\;\; u_i \;\; v_i$
資料範圍:
- $3 \le n \le 100\,000$。
- $0 \le u_i < v_i \le n-1$($1 \le i \le n-3$)。
- 保證所有線段皆不會在端點之外相交。
- 輸入的數字都是整數。
Output Format
- line $1+i$ ($0 \le i \le n-3$): $\;\; q_i$
Sample Input 1
3
Sample Output 1
3
Sample Input 2
6 0 2 0 4 0 3
Sample Output 2
6 14 30 55
Sample Input 3
7 0 2 3 5 2 6 2 5
Sample Output 3
7 17 39 79 144
Sample Input 4
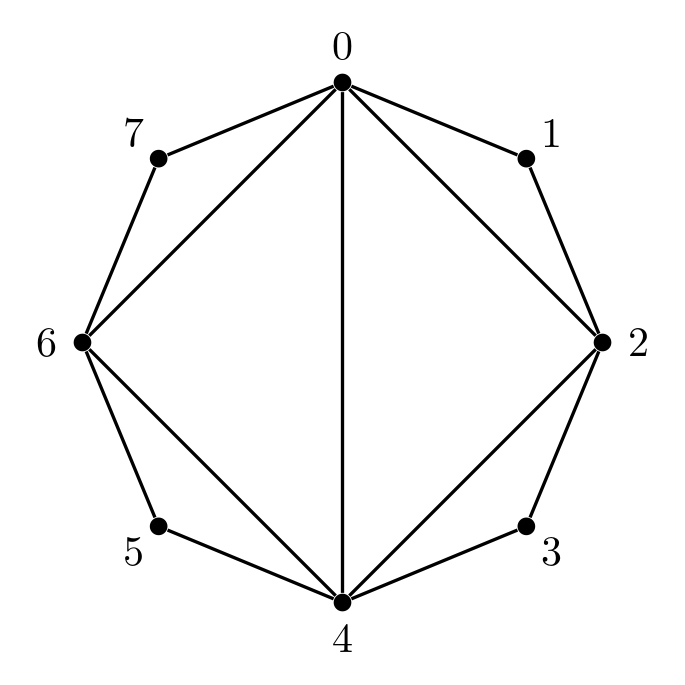
8 4 6 0 4 0 2 0 6 2 4
Sample Output 4
8 20 52 112 204 360
Hints
範例一
該輸入滿足子任務 1, 2, 3, 4, 5, 6, 8 的限制。
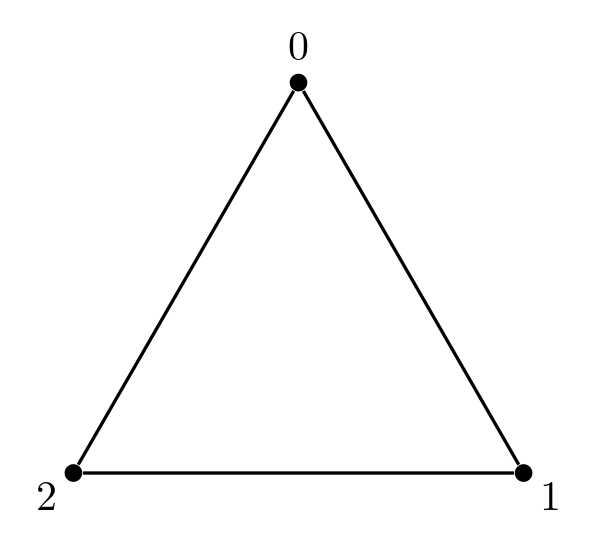
在該圖形中拿掉任意一條邊都會形成一棵樹,因此他的生成樹總共有 $3$ 種。
範例二
該輸入滿足子任務 1, 2, 3, 4, 5, 6, 8 的限制。
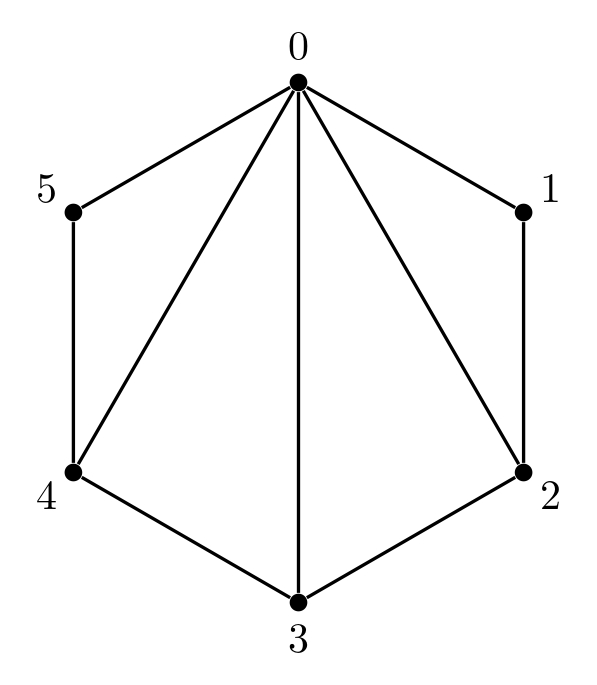
在加入 $(0, 2)$ 這條邊之後,生成樹的數量為 $6 + 8 = 14$:
- 沒有包含 $(0, 2)$:$6$ 種生成樹。
- 有包含 $(0, 2)$:要在 $(0, 1)$ 跟 $(1, 2)$ 之間丟掉一條邊;也要在 $(2, 3)$、$(3, 4)$、$(4, 5)$、$(0, 5)$ 之間丟掉一條邊,共有 $2 \times 4 = 8$ 種生成樹。
範例三
該輸入滿足子任務 1, 2, 3, 5, 6, 8 的限制。
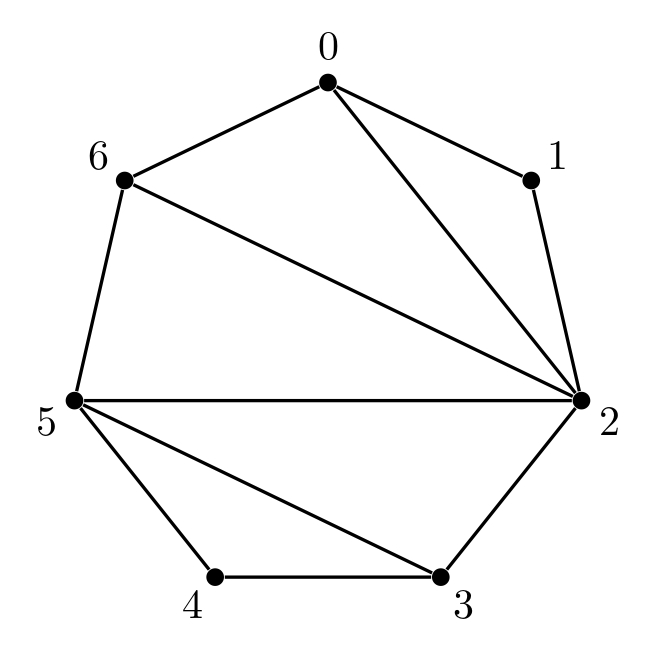
範例四
該輸入滿足子任務 1, 2, 3, 5, 6, 7, 8 的限制。
Problem Source
YTP 2025 高中組程式挑戰營 p19
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 80~83 | 範例測試資料。 | 0 |
| 2 | 0~7, 80~83 | $n \le 10$。 | 1 |
| 3 | 0~17, 80~83 | $n \le 80$。 | 4 |
| 4 | 0~27, 80~83 | $n \le 400$。 | 2 |
| 5 | 28~33, 80~81 | $n \le 2000$、$u_i = 0$($1 \le i \le n-3$)。 | 2 |
| 6 | 0~43, 80~83 | $n \le 2000$。 | 5 |
| 7 | 0~50, 80~83 | $n \le 40\,000$。 | 7 |
| 8 | 51~72, 83 | $n$ 是 $2$ 的正整數冪次、對所有 $k = 1, 2, \ldots, (\log_2 n)-1$ 以及 $a = 0, 1, \ldots, \frac{n}{2^ k}-1$ 皆存在一條連接 $a 2^ k$ 及 $(a+1) 2^ k \bmod n$ 的邊。 | 3 |
| 9 | 0~83 | 無額外限制。 | 1 |
