975 . 守望相助
TopCoder
Tags
Description
在 YTP 小鎮中,有 $n$ 個駐紮點可以讓警衛駐守,分別由 $1$ 編號到 $n$。某些駐紮點之間由道路連接,我們稱這樣的駐紮點相鄰,共有 $m$ 條道路。
小鎮需要安排警衛駐守這些駐紮點。每位警衛只能駐守在一個駐紮點上,而一位警衛所能守衛的範圍是他所在的駐紮點,以及與他所在駐紮點相鄰的所有駐紮點。
為了避免警衛之間干擾或重複守衛的資源浪費,規定兩位警衛不能駐紮在彼此相鄰的兩個駐紮點上。
你需要找出所有的「合法配置」,即符合下列條件的駐紮點集合 $S$:
- 所有駐紮點(從 $1$ 到 $n$)都必須在至少一位警衛的守衛範圍中
- $S$ 中的任意兩個駐紮點,彼此不相鄰
- $S$ 中無法再加入任何其他駐紮點而同時仍然滿足前兩個條件
請你找出所有這樣的集合 $S$,並將其中的駐紮點編號由小到大排序後輸出。
若有多個符合條件的 $S$,請按字典序遞增排序全部輸出。
註:
集合的字典序遞增排序,是指將集合中的元素視為有序數列(例如以升序排列),並根據字典序進行排序。
更正式地說,給定二集合 $A, B$ ,將他們都表示為一個升序排列的序列
- $A = \lbrace a_1, a_2, \dots, a_m\rbrace$ 且 $a_1 < a_2 < \dots < a_m$
- $B = \lbrace b_1, b_2, \dots, b_n\rbrace$ 且 $b_1 < b_2 < \dots < b_n$
我們說 $A$ 在字典序上小於 $B$,當且僅當存在某個索引 $t$,使得以下其中一種情況成立:
- 對所有 $1 \leq s < t \leq \min(m, n)$ ,有 $a_s = b_s$ 且 $a_t < b_t$。
- 對所有 $1 \leq s \leq m < n$ ,有 $a_s = b_s$,即 $A$ 為 $B$ 的前綴。
若一個集合序列依此順序排列,則稱其為集合的字典序遞增排序。
例如:
- $\lbrace 1,3,5\rbrace$ 在字典序上小於 $\lbrace 1,4\rbrace$,因為第二個位置上 $3 < 4$。
- $\lbrace 1,2\rbrace$ 在字典序上小於 $\lbrace 1,2,3\rbrace$,因為前者是後者的前綴。
Input Format
第一行有兩個整數 $n, m$ , $n$ 代表駐紮點數量, $m$ 代表道路數量。
接下來的 $m$ 行,每行有兩個正整數 $x, y$ ,表示駐紮點 $x$ 與駐紮點 $y$ 相鄰。
- $1 \le n \le 20$
- $0 \le m \le \frac{n(n-1)}{2}$
- $1 \le x, y \le n$, $x \neq y$
- $(x, y)$ 不會重複出現, $(x, y)$ 與 $(y, x)$ 視為相同
Output Format
每一行輸出一組合法的駐紮點集合 $S$,元素依序由小到大排列,元素間以空格分隔。
若有多組 $S$ ,按字典序由小到大排列整個集合。
Sample Input 1
5 5 1 2 2 5 3 1 4 5 4 3
Sample Output 1
1 4 1 5 2 3 2 4 3 5
Sample Input 2
7 5 1 2 4 2 5 6 1 3 7 5
Sample Output 2
1 4 5 1 4 6 7 2 3 5 2 3 6 7 3 4 5 3 4 6 7
Sample Input 3
1 0
Sample Output 3
1
Hints
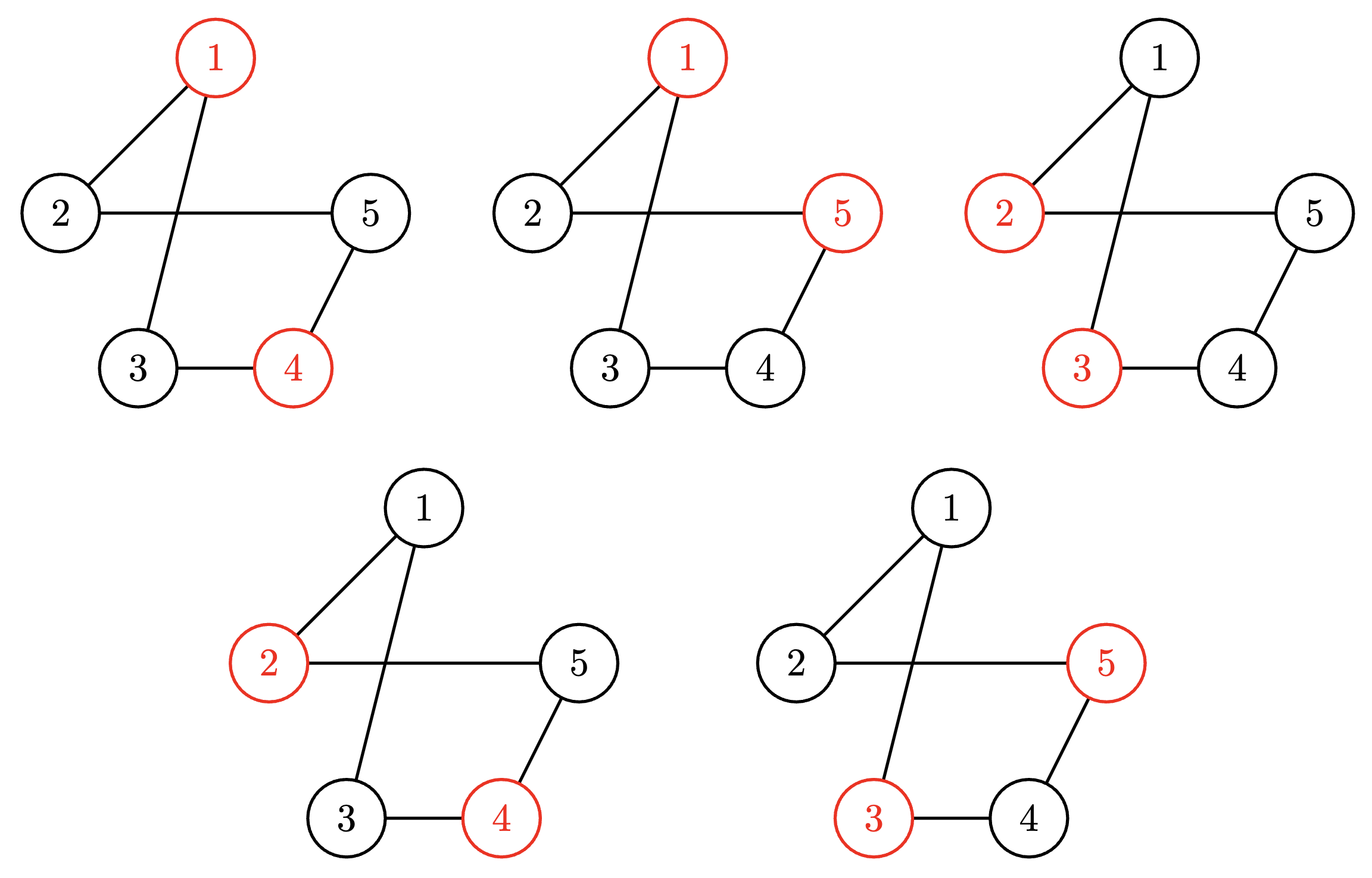
範例1如圖所示。
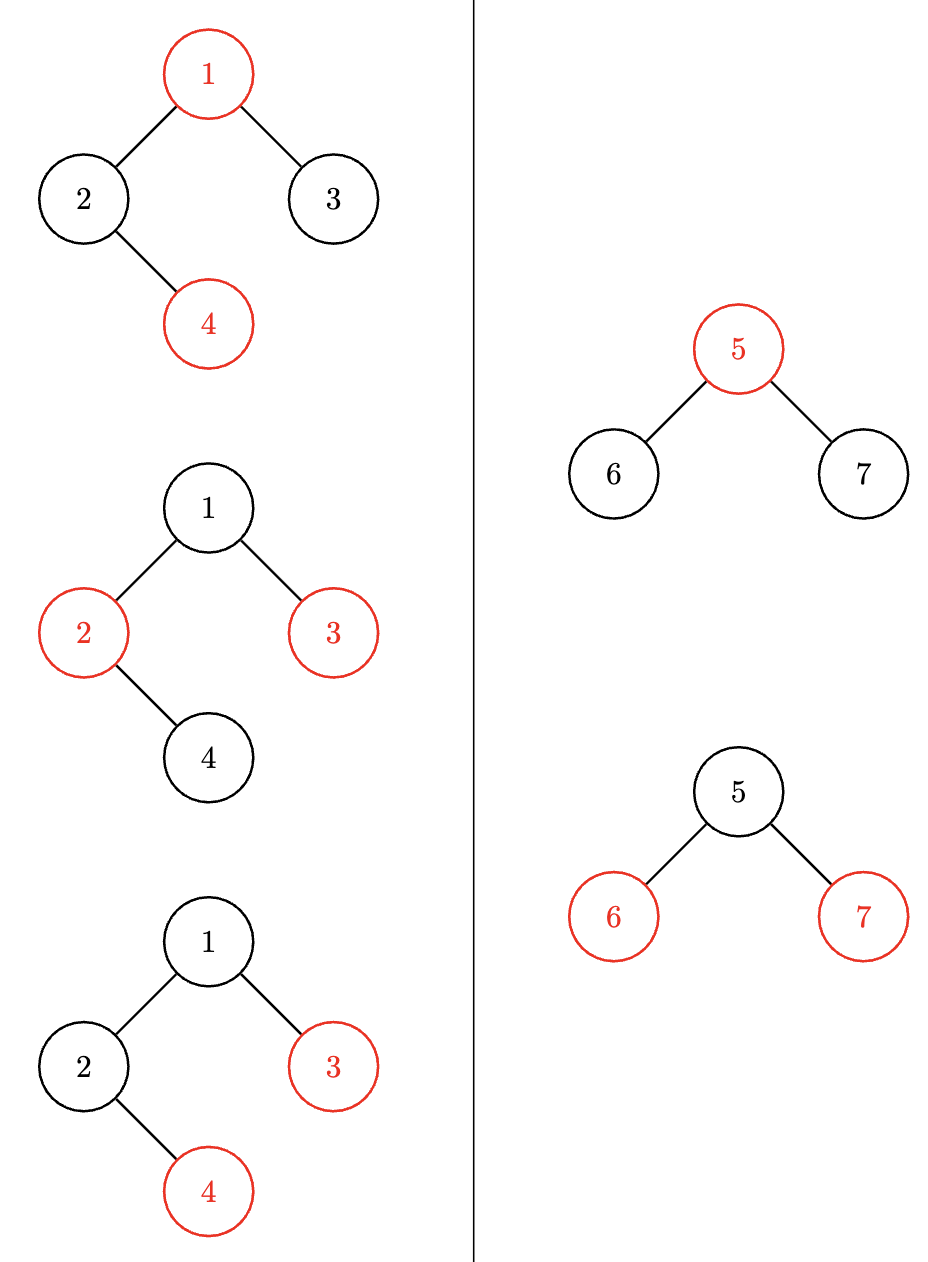
範例2中的各連通塊之 $S$ 為 $\lbrace \lbrace 1,4\rbrace ,\lbrace 2,3\rbrace , \lbrace 3,4\rbrace \rbrace , \lbrace \lbrace 5\rbrace , \lbrace 6,7\rbrace \rbrace $,在這組測資中,合法的 $S$ 為各連通塊之 $S$ 的笛卡爾積。
笛卡爾積說明:笛卡爾積是指從每個集合中各取一個元素並組合它們。在此例中,我們從 $\lbrace \lbrace 1,4\rbrace ,\lbrace 2,3\rbrace , \lbrace 3,4\rbrace \rbrace $ 中選一個集合,從 $\lbrace \lbrace 5\rbrace , \lbrace 6,7\rbrace \rbrace $ 中選一個集合,總共有 $3 \times 2 = 6$ 種可能的組合:
- $\lbrace1,4\rbrace \cup \lbrace5\rbrace = \lbrace1,4,5\rbrace$
- $\lbrace1,4\rbrace \cup \lbrace6,7\rbrace = \lbrace1,4,6,7\rbrace$
- $\lbrace2,3\rbrace \cup \lbrace5\rbrace = \lbrace2,3,5\rbrace$
- $\lbrace2,3\rbrace \cup \lbrace6,7\rbrace = \lbrace2,3,6,7\rbrace$
- $\lbrace3,4\rbrace \cup \lbrace5\rbrace = \lbrace3,4,5\rbrace$
- $\lbrace3,4\rbrace \cup \lbrace6,7\rbrace = \lbrace3,4,6,7\rbrace$
範例3中只有一個駐紮點,所以合法的 $S$ 中只有那個點。
Problem Source
YTP 2025 國中組程式挑戰營 p5
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~2 | 範例測試資料 | 0 |
| 2 | 0~24 | 無額外限制 | 15 |
