978 . 橢圓曲線數位簽章演算法
TopCoder
Tags
Description
ECDSA(Elliptic Curve Digital Signature Algorithm,橢圓曲線數位簽章演算法)是一個基於橢圓曲線密碼學的數位簽章演算法,他讓傳送方可以用私人密鑰簽名資料,並讓接受方用公開密鑰驗證簽名確實是來自於傳送方,以及驗證內容是否被竄改。ECDSA 比起傳統的 DSA/RSA 等算法有更好的安全性,因此在密碼學中有很重要的功能。
首先先來介紹一下橢圓曲線。一個橢圓曲線的定義是 $y^ 2 = x^ 3 + ax + b$,其中 $a, b$ 是橢圓曲線的參數,且滿足 $-16(4a^ 3 + 27b^ 2) \neq 0$。如果你覺得很奇怪,這條式子是為了保證橢圓曲線沒有尖點與自交點,但那超出本題範圍了。
下面是一條橢圓曲線 $y^ 2 = x^ 3 - 11x + 1$ 畫在二維座標平面的樣子:
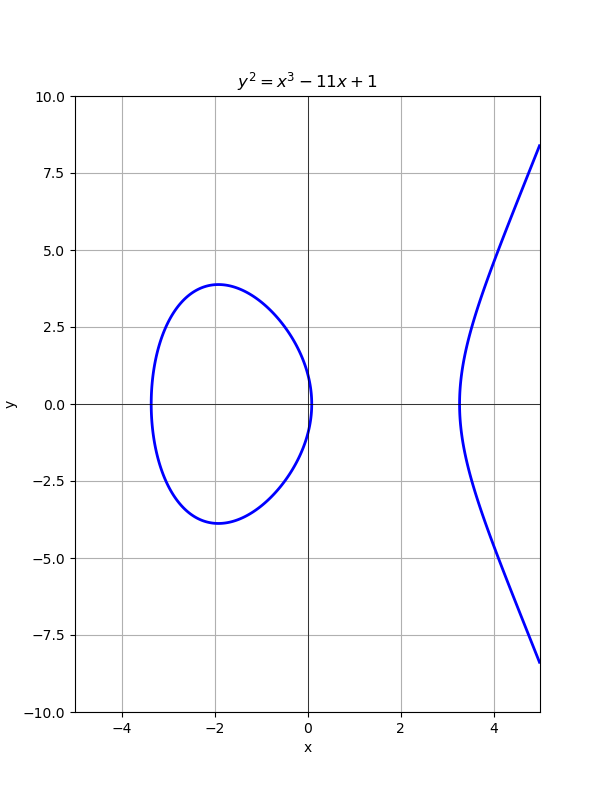
左邊的那個圖形其實不是橢圓,「橢圓曲線」這個名稱跟幾何上的橢圓一點關係也沒有,純粹是歷史原因。
我們接著把橢圓曲線上面的所有點收集起來形成一個集合。在進入演算法之前,我們要先來定義如何在這個集合裡做一些運算。
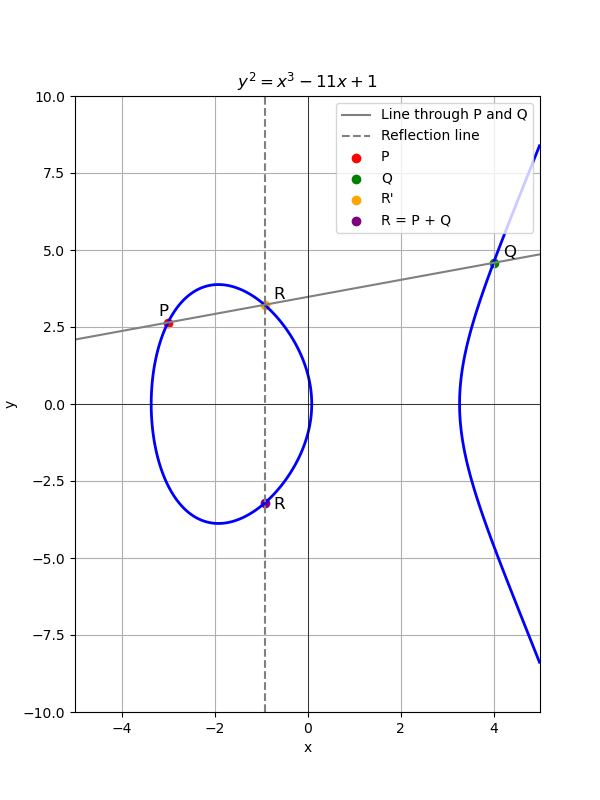
首先是橢圓曲線上面的點加法:假設有兩個點 $P(x_1, y_1), Q(x_2, y_2)$,那麼定義 $R(x_3, y_3) = P+Q$,使得 $P, Q, R'$ 三點共線,且 $R$ 為 $R'$ 對 $x$ 軸的對稱點(注意到橢圓曲線上任一點的對稱點也會在橢圓曲線上)。
具體上是怎麼做的呢?我們把 $\overleftrightarrow{PQ}$ 的方程式算出來,斜率就是 $s = \frac{y_2 - y_1}{x_2 - x_1}$,因此直線方程式是 $y = s(x-x_1) + y_1$,要得到交點 $R'(x_3, y_3')$,我們把直線代進橢圓曲線的方程式:
$$(s(x-x_1) + y_1)^ 2 = x^ 3 + ax + b$$
到這裡你有兩種方法,一種是直接炸開那個方程式,但計算很繁瑣。因此我們採用第二種方法:根與係數來計算。上面那個方程式已經有兩個根分別是 $P(x_1, y_1)$ 以及 $Q(x_2, y_2)$ 了。根據韋達定理,我們知道 $x_1 + x_2 + x_3 = s^ 2$(看二次項的係數),因此 $x_3 = s^ 2 - x_1 - x_2$,而代回直線方程式就有 $y_3' = s(x_3 - x_1) + y_1$。但是且慢!這裡算出來的東西是 $R'$,想得到 $R$ 我們還要對他對 $X$ 軸做對稱,因此最後的結果是 $y_3 = s(x_1 - x_3) - y_1$,這樣就完成兩個點的加法了。
還有幾點補充,首先上述的式子在 $x_1 = x_2$ 時會錯,此時我們要看 $y_1$ 與 $y_2$ 的情況,可以證明只有兩種可能:
- 首先如果 $y_1 = -y_2$,那代表著 $P$ 跟 $Q$ 是對於 $x$ 軸對稱,那此時我們畫一條鉛直線,你會發現這個鉛直線只跟橢圓曲線有兩個交點,怎麼辦?為了解決這個弔詭的狀況,數學家們定義出了一個點,稱呼為無窮遠點 $\mathcal{O}$,這個點不會有個實際的座標,並且他同時會被所有鉛直線經過。那麼此時我們就可以說 $P + Q = \mathcal{O}$ 了。
- 而對於另外一種情況 $y_1 = y_2$,我們會把 $s$ 定義成切線斜率,這樣會得到 $s = \frac{3x_1^ 2 + a}{2y_1}$,剩下的 $x_3, y_3$ 等的計算方式跟上面的一樣。
- 你可能已經發現了,如果 $y_1 = y_2 = 0$ 怎麼辦呢,如果你把鉛直線的斜率視為無窮大(或負無窮大),那麼用第一種情況可以直接得到 $P + Q = \mathcal{O}$,而在第二種情況時,你畫出的切線依然是鉛直線,所以不管用哪種方式定義都會得到 $P + Q = \mathcal{O}$ 了,好耶。
最後,$\mathcal{O}$ 也是可以放在等式的左邊的,對於所有 $P$,$\mathcal{O} + P = P$,同理 $P + \mathcal{O} = P$,這樣所有狀況就都被處理完了。(你可以想像 $\mathcal{O}$ 相當於整數加法上的 $0$,而把一個點對 $x$ 軸做對稱相當於對他取負號)。
接下來我們要來解釋要怎麼把一個數乘上一個點,他可以如下遞迴定義:$0 \ast P = \mathcal{O}, k \ast P = P + (k-1) \ast P$,也就是說他就只是 $P$ 累加 $k$ 次而已,雖然這題不會用到,但我們可以類似的定義負數的 $k$,$k \ast P$ 是使得 $k \ast P + (-k) \ast P = \mathcal{O}$ 成立的唯一一個點以達到類似的目的。
接下來我們來把這個橢圓曲線放進模 $M$ 的世界中,其中 $M$ 是一個質數。在這個世界裡面所有加法,乘法等操作都在模 $M$ 下進行。假設 $M = 17$ ,那麼上面那條橢圓曲線的樣子如下圖:
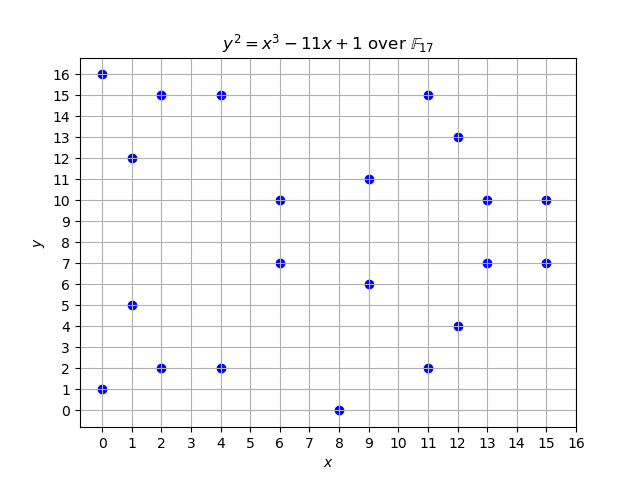
代表說總共有 $21$ 個點滿足這條曲線方程式,如果我們照上面的方式收集所有的點,加上無窮遠點,總共會得到 $22$ 個點,這 $22$ 個點就形成這個橢圓曲線在 $M = 17$ 底下的解集合。
你或許會注意到 $22$ 這個數字很接近剛剛的 $M = 17$,這並不是巧合,根據 Hasse 定理,假設橢圓曲線的根集有 $N$ 個點(含無窮遠點 $\mathcal{O}$),那麼以下不等式成立:
$$|N - (M+1)| \leq 2 \sqrt{M}$$
這代表根集的大小不會跟模數 $M$ 差太多。
對了,如果你很疑惑應該要怎麼在模 $M$ 底下算除法,以下是一個簡單的說明。在模 $M$ 底下的 $\frac{a}{b}$ 被定義成 $a \times b^ {-1}$,其中 $b^ {-1}$ 是一個介在 $[0, M-1]$ 的整數,使得 $b \times b^ {-1} \equiv 1 \pmod{M}$。在 $M$ 是質數,並且 $b \neq 0$ 的情況我們可以利用費馬小定理:$b^ {M-1} \equiv 1 \pmod{M}$。這個定理告訴我們 $b \times b^ {M-2} \equiv 1 \pmod{M}$,因此 $b^ {-1} \equiv b^ {M-2} \pmod{M}$。
為了讓你更容易理解這段在幹嘛,我們來實際操作一下兩個點的加法。假設 $P = (1, 5)$,$Q = (13, 7)$,我們想要算出 $R(x_3, y_3) = P + Q$。首先先算出 $s$,$s = \frac{7-5}{13-1} = \frac{1}{6}$,但我們要把他換成模 $M = 17$,因此 $s = \frac{1}{6} \equiv 1 \times 6^ {-1} \equiv 1 \times 6^ {17-2} \equiv 1 \times 3 \equiv 3 \pmod{M}$,因此 $s = 3$,那麼就有 $x_3 = s^ 2 - x_1 - x_2 = 9 - 1 - 13 = 12$,然後 $y_3 = 3(1 - 12) - 5 = 13$,因此 $P + Q = (12, 13)$。
現在我們終於要來解釋這樣定義完橢圓曲線上面點的加法跟點與常數的乘積後要幹嘛了。我們要解決的問題是,現在有兩個人 Alice 跟 Bob 要傳訊息,但是他們只能在公開的網路上傳,因此他們必須防止 Alice 傳給 Bob 的訊息被中間人 Oscar 截獲並偽造成 Alice 傳的訊息,否則 Bob 就不知道訊息是否真的是來自 Alice 的了。為了解決這個問題,密碼學家們發展出了數位簽章技術,可以讓 Alice 對 Bob 證明發送這個訊息的確是來自 Alice 而不是 Oscar。
製作簽章的過程按照以下步驟:
- 首先 Alice 和 Bob 要先共同決定一個橢圓曲線 $CURVE$,這個曲線上的任意一點 $G$,以及一個數字 $n$,其中 $n$ 是最小的正整數使得 $n \ast G = \mathcal{O}$,並且 $n$ 是一個質數。兩個人彼此知道這些參數 $(CURVE, G, n)$。
- 接下來 Alice 在 $[1,n-1]$ 裡面決定一個私鑰 $d$,這個 $d$ 只被自己知道,並把公鑰 $Q = d \ast G$ 公布在網路上,因此 Bob 也會知道公鑰。
- 然後 Alice 再在 $[1,n-1]$ 裡面選擇一個隨機數 $k$,並計算 $(x_1, y_1) = k \ast G$,
- 他接著算出 $r = x_1 \bmod n$ 以及 $s = k^ {-1}(z+rd) \bmod n$,其中 $z$ 是他要傳的訊息。這裡的 $k^ {-1}$ 的求法一樣可以利用費馬小定理。
- 最後 $(r,s)$ 就是他傳出的簽章。
在一般情況下 $z$ 會是訊息經過雜湊之後轉成的一個整數值,但在這題中為了簡化我們假設 $z$ 就是訊息本身。
至於 Bob 收到這個簽章之後的驗證方式呢?很簡單:
- 首先算出 $t = z \times s^ {-1} \bmod n$ 與 $u = r \times s^ {-1} \bmod n$,
- 接著計算 $v = x_2 \bmod n$,其中 $(x_2, y_2)$ 是 $t \ast G + u \ast Q$ 的座標,
- 最後驗證 $v$ 是否等於 $r$ 即可,簽章被接受當且僅當 $v = r$ 成立。
好了,現在你已經會製作簽章跟驗證簽章了,但是 Alice 還不會。她已經決定好了橢圓曲線 $CURVE$ 跟其上一點 $G$,但是她忘記 $n$ 是多少了,因此 $n$ 只能由你自己算出來了。另外她也決定好了私鑰 $d$,隨機數 $k$,以及訊息 $z$,現在請你幫她製作一個簽章,讓她可以順利的傳訊息給 Bob。
最後再提一點,一般情況下,為了順利解密,要是在上面的過程中,算出的 $r$ 或 $s$ 是 $0$,則 Alice 要退回選隨機數的步驟並重選一個 $k$。但是在本題我們忽略這個步驟,也就是說不管你簽名的 $r$ 以及 $s$ 是不是 $0$,都直接輸出即可。
Input Format
輸入只有一行,包含八個以空白分隔的整數 $M, a, b, G_x, G_y, d, k, z$。
其中:
- $CURVE$ 是 $y^ 2 = x^ 3 + ax + b$ 這個方程式
- 基點 $G$ 的座標是 $(G_x, G_y)$。
資料範圍:
- $17 \leq M \leq 2 \times 10^ 5$
- $0 \leq a, b, G_x, G_y < M$
- $1 \leq d, k < n$
- $0 \leq z < n$
- 保證 $M$ 是一個質數
- 保證 $-16(4a^ 3 + 27b^ 2) \not\equiv 0 \pmod{M}$
- 保證 $G$ 在 $CURVE$ 上
- 保證 $n$ 是一個質數
Output Format
輸出兩個以空白隔開的非負整數 $r, s$,代表你製作的簽章。
Sample Input 1
17 6 1 12 13 5 7 9
Sample Output 1
4 1
Hints
在範例測試資料中,橢圓曲線的方程式是 $y^ 2 = x^ 3 + 6x + 1$,在模 $17$ 底下進行。兩人取的 $G$ 是 $(12, 13)$ 這個點。
稍做一些計算可以得到 $n = 11$。具體方式如下(以下所有的操作都考慮在模 $17$ 下執行):
- 要計算 $2 \ast G = G + G$,我們有 $x_1 = x_2 = 12, y_1 = y_2 = 13$,這樣可以得到 $s = \frac{3x_1^ 2+a}{2y_1} = \frac{13}{9} = 9$,因此假設 $2 \ast G$ 的座標是 $(x_3, y_3)$,那麼 $x_3 = 9^ 2 - 12 - 12 = 6$,$y_3 = 9(12-6) - 13 = 7$,所以 $2 \ast G = (6, 7)$。
- 要計算 $3 \ast G = G + 2 \ast G$,我們有 $x_1 = 12, y_1 = 13, x_2 = 6, y_2 = 7$,此時 $s = \frac{7-13}{6-12} = 1$,因此同樣假設 $3 \ast G$ 的座標是 $(x_3, y_3)$,那麼 $x_3 = 1^ 2 - 12 - 6 = 0$,$y_3 = 1(12-0) - 13 = 16$,所以 $3 \ast G = (0, 16)$。
- 接下來 $4 \ast G = (4, 2)$,$5 \ast G = (9, 6)$,$6 \ast G = (9, 11)$,$7 \ast G = (4, 15)$,$8 \ast G = (0, 1)$,$9 \ast G = (6, 10)$,$10 \ast G = (12, 4)$。
- $11 \ast G = G + 10 \ast G$,此時發現這兩個點的 $x_1 = x_2, y_1 = -y_2$,因此 $11 \ast G = \mathcal{O}$,所以最小的正整數 $n$ 使得 $n \ast G = \mathcal{O}$ 是 $n = 11$。
接著計算:
- $k \ast G = 7 \ast G = (4, 15)$
- $r = 4 \bmod 11 = 4$
- $s = k^ {-1}(z+rd) \bmod n = 8 \times (9 + 4 \times 5) \bmod 11 = 1$
因此輸出 4 1。
Problem Source
YTP 2025 國中組程式挑戰營 p8
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0 | 範例測試資料 | 0 |
| 2 | 0~32 | 無額外限制 | 20 |
