979 . 幻境之心
TopCoder
Tags
Description
在幻境群島的中心,聳立著一座傳說中的浮空晶塔,裡面封印著一顆擁有巨大魔力的寶石:幻境之心。
千年來,幻境群島上的村莊靠著幻境之心散發出的保護結界,抵禦著黑霧魔獸的侵襲。
然而,如今幻境之心能量衰退,晶塔僅能夠釋放出一枚移動式魔法結界球,結界球將漂浮於任意一座村莊上空,並釋放半徑為 $R$ 的圓形魔法護盾,守護附近的村莊。
但魔法是有代價的:
- 施展半徑為 $R$ 的護盾需要消耗 $R^ 2$ 單位的魔力。
- 每一座未被護盾覆蓋的村莊,會受到黑霧侵蝕,造成 $C$ 單位的損失。
作為新任的魔導工程師,你的任務是決定:
- 將結界球部署在哪一座村莊的上空
- 設定護盾半徑 $R$
以最小化整體損耗:$\text{總損耗} = R^ 2 + C \times \text{未被護盾覆蓋的村莊數量}$。
給定幻境群島上 $n$ 座村莊的座標,你可以選擇其中一座村莊為結界球的部署位置,並設定護盾半徑 $R$。
所有與圓心距離小於等於 $R$ 的村莊會受到護盾保護,即 $(X - x_i)^ 2 + (Y - y_i)^ 2 \leq R^ 2$ 將被保護,其中 $(X, Y)$ 是結界球的座標,$(x_i, y_i)$ 是第 $i$ 座村莊的座標。
未被保護的村莊數量將造成額外損耗。
請你計算 整數 半徑 $R$,使得此半徑下的總損耗最小並輸出總損耗。
Input Format
輸入的第一行包含兩個正整數 $n, C$,代表村莊的數量和每座未被護盾覆蓋的村莊所造成的損失。
接下來的 $n$ 行,每行包含兩個整數 $x_i, y_i$,代表第 $i$ 座村莊的座標。
- $1 \leq n \leq 1000$。
- $1 \leq C \leq 10^ 9$。
- $-10^ 6 \leq x_i, y_i \leq 10^ 6$ ($1 \leq i \leq n$)。
- 所有的 $(x_i, y_i)$ 都不相同。也就是說,對於任意 $i \neq j$,$(x_i, y_i) \neq (x_j, y_j)$。
Output Format
輸出一行,包含一個整數,代表最佳整數半徑下的總損耗。
Sample Input 1
4 100 0 0 10 0 0 10 10 10
Sample Output 1
200
Sample Input 2
5 5 0 0 2 0 0 2 2 2 5 5
Sample Output 2
14
Sample Input 3
6 50 0 0 1 0 2 0 10 0 11 0 12 0
Sample Output 3
100
Hints
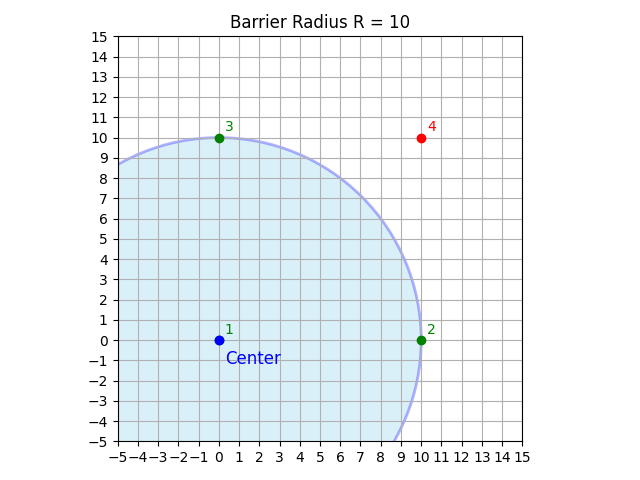
在範例 1 中,最佳的結界球部署位置是任意一個角落村莊,護盾半徑 $R = 10$,總損耗為 $200$。如圖所示:
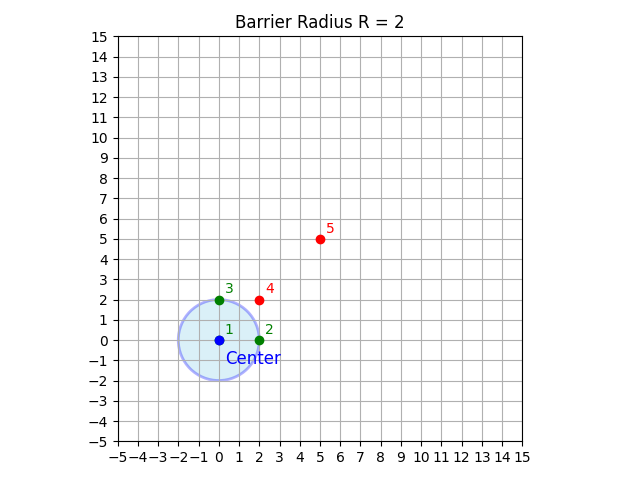
在範例 2 中,最佳的結界球部署位置是 $(0, 0)$,護盾半徑 $R = 2$ 或 $R = 3$,總損耗為 $14$。如圖所示:
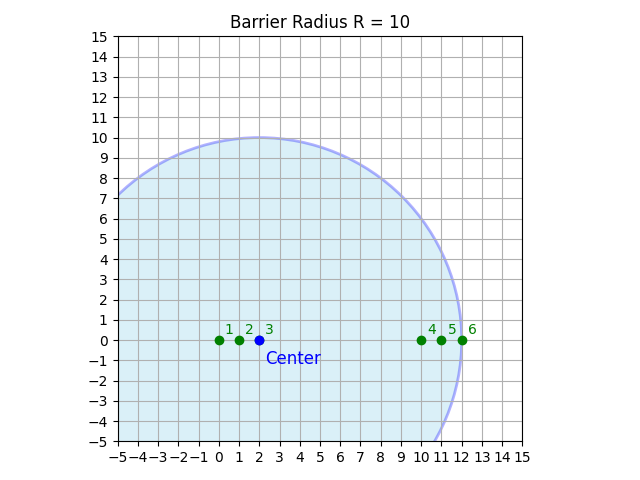
在範例 3 中,最佳的結界球部署位置是 $(2, 0)$ 或 $(10, 0)$,護盾半徑 $R = 10$,總損耗為 $100$。如圖所示:
Problem Source
YTP 2025 國中組程式挑戰營 p9
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~2 | 範例測試資料 | 0 |
| 2 | 0~55 | 無額外限制 | 20 |
