980 . 雲彩公園
TopCoder
Tags
Description
在天空之城中,共有 $n$ 座公園與 $m$ 條道路連接這些公園。每座公園中,都有一隻供遊客觀賞的幼獨角獅,共有 $k$ 種不同顏色。
每座公園 $i$ 擁有一隻顏色為 $c_i$ 的幼獨角獅。若有一條道路連接兩座公園,則這兩座公園互為相鄰。
如果相鄰的兩座公園中,幼獨角獅的顏色相同,遊客可能會因此感到困惑,我們稱這種情況為混淆。
天空之城的管理者 ── 爸爸精靈 ── 注意到紅色與藍色的幼獨角獅特別受到遊客歡迎,因此決定將所有幼獨角獅重新染色,僅使用「紅色」與「藍色」這兩種顏色。
然而,若不經規劃地隨意染色,可能會導致混淆。因此爸爸精靈計劃對整座城市的交通進行調整,具體作法如下:
- 將原本的 $m$ 條道路劃分為 $p$ 條觀光路線
- 每條道路必須恰好被分配到一個觀光路線中
- 每條觀光路線至少有一條道路
- 每天開放一條觀光路線時,遊客只能走在這條路線上的道路
- 如果可以針對每條觀光路線,為所有公園中的獨角獅指定紅或藍,使得該路線內不會出現任何相鄰公園擁有相同顏色的幼獨角獅的情形,那麼此觀光路線即視為合法
為了避免觀光路線過多,爸爸精靈至多能劃分為 $\lceil \log_{2} k \rceil$ 條觀光路線。由於天空之城實在過於廣大,他決定拜託你協助進行這項劃分規劃。
可以證明,在以上的條件下必定有一種合法的劃分方式。
Input Format
第一行有三個正整數 $n, m, k$,分別代表公園的數量、道路的數量以及幼獨角獅的顏色種類數。
第二行有 $n$ 個正整數 $c_1, c_2, \ldots, c_n$,其中第 $c_i$ 代表公園 $i$ 中幼獨角獅的顏色。
接下來有 $m$ 行,每行兩個正整數 $u_j, v_j$,代表第 $j$ 條道路連接公園 $u_j$ 和公園 $v_j$
- $2 \le n \le 10^ 5$
- $n-1 \le m \le \max(\frac{n(n-1)}{2}, 10^ 5)$
- $2 \le k \le n$
- $1 \le c_i \le k$
- $(u_j, v_j) \neq (u_k, v_k) \text{ if } j \neq k$
- $c_{u_j} \neq c_{v_j} \forall j$
Output Format
第一行輸出一個正整數 $p (1 \sim \lceil \log_2 k \rceil)$,代表有幾條觀光路線。
然後對於 $p$ 條旅遊路線中的每一條:
先輸出一行 $s_i$,代表該觀光路線包含的道路數量。
接下來再輸出 $s_i$ 行,每行兩個正整數 $u_j, v_j$,代表該觀光路線包含的道路。
每個原先給定的道路都必須出現在恰好一條觀光路線中。
Sample Input 1
8 13 4 1 2 1 3 2 4 1 3 1 2 1 5 1 8 2 3 2 6 2 8 3 4 3 5 3 8 4 6 5 6 6 7 6 8
Sample Output 1
2 8 1 2 1 5 2 3 2 8 3 5 4 6 6 7 6 8 5 1 8 2 6 3 4 3 8 5 6
Hints
如圖所示,最上方為範例測資 1 的圖例。
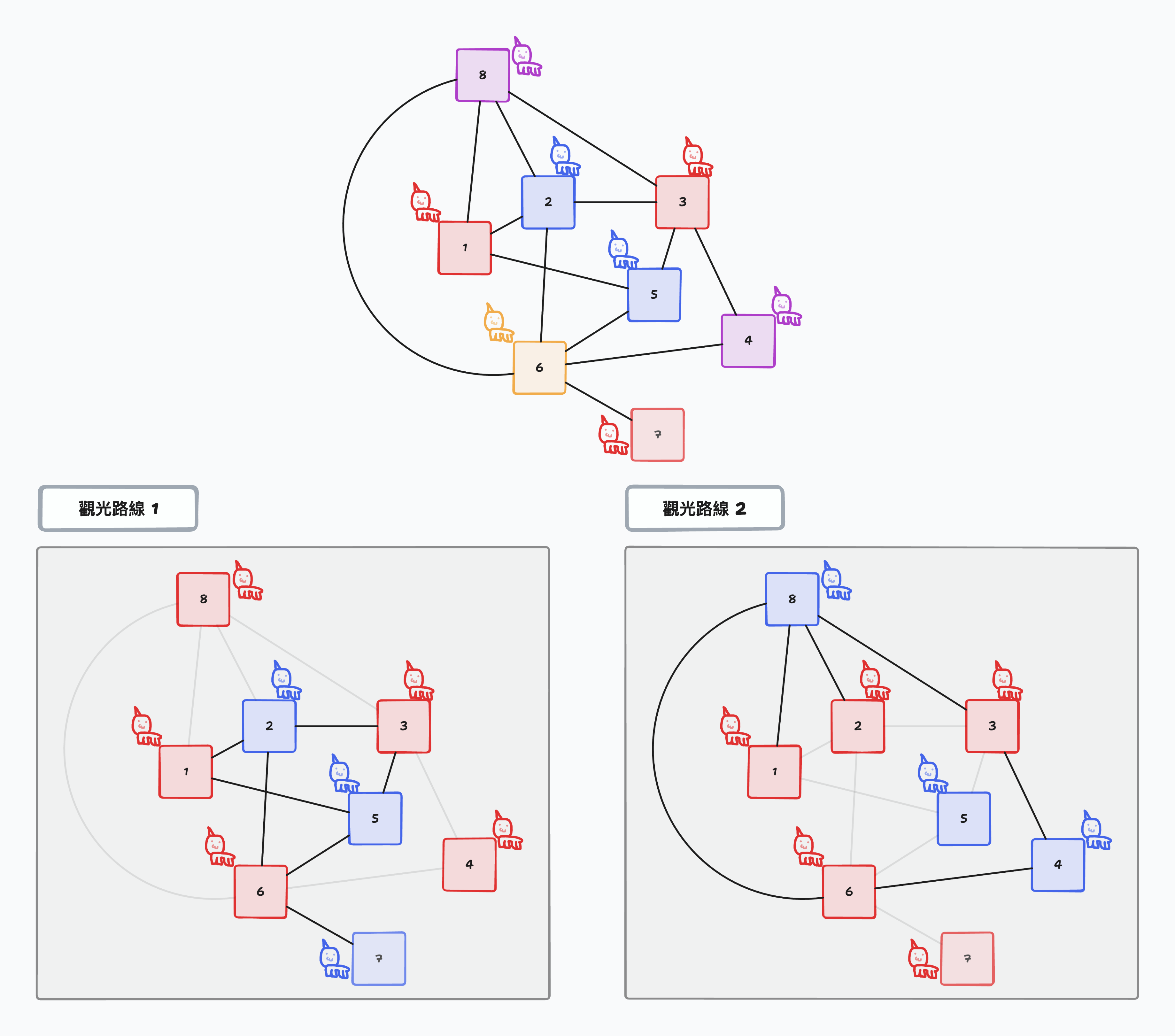
在觀光路線 1 中,包含了道路 $(1, 2)$、$(1, 5)$、$(2, 3)$、$(2, 6)$、$(3, 5)$、$(5, 6)$、$(6, 7)$ 這 $7$ 條道路。
在觀光路線 2 中,包含了道路 $(1, 8)$、$(2, 8)$、$(3, 4)$、$(3, 8)$、$(4, 6)$、$(6, 8)$ 這 $6$ 條道路。
對於這兩條觀光路線,我們都有辦法找到僅使用紅、藍兩色將幼獨角獅染色,且沒有相鄰的兩個公園的幼獨角獅顏色相同,因此這兩條觀光路線都是合法的。
Problem Source
YTP 2025 國中組程式挑戰營 p10
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0 | 範例測試資料 | 0 |
| 2 | 0~9 | $k \le 4$ | 6 |
| 3 | 0~39 | 無額外限制 | 14 |
