983 . 立竿見影
TopCoder
Tags
Description
在一個廣闊的大草原裡,有一隻大獅子時常在上面奔跑追捕獵物,從日出到日落。有一天,他發現到太陽照射到物品會產生影子,並且會隨著時間改變角度以及長度,因此他決定要來做實驗去觀察這個現象。他撿了幾根細長的棍子,計算好每一根棍子的高度還有座標位置,並且做完了實驗和收集數據。當他興高采烈的跑去跟好朋友大老虎說的時候,突然發現他辛苦收集的數據不見了,由於他不想要被大老虎嘲笑,因此希望你可以透過你的數學知識幫助大獅子假造一份實驗數據。
大獅子選定了一批實驗用的 $N$ 根棍子,在計算完棍子的數據後會將每一根棍子的高度和位置告訴你,他在之前一共進行了 $Q$ 次的實驗,在之前的實驗中,大獅子會觀察每次太陽照射後,影子是向棍子右或是向左延伸,以及影子長度和棍子長度的比值是多少,大獅子希望你幫他算出在這樣的條件下,產生出影子的全部交集長度會是多少,對於每一次的實驗都需要算出答案。
Input Format
第一行會輸入兩個正整數 $N, Q$,代表樹枝的數量和詢問的次數。
第二行會輸入 $N$ 個整數 $x_i$,代表樹枝的 x 座標,$x_i$ 會兩兩相異,$x$ 座標向右為正。
第三行會輸入 $N$ 個正整數 $h_i$,代表樹枝的高度。
第四行會輸入 $Q$ 個整數 $q_i$,代表大獅子需要你幫忙計算當樹枝影子長度為樹枝高度的 $q_i$ 倍時,總共的影子長度為多少。當 $q_i > 0$ 時代表此時竿子影子向右, $q_i < 0$ 代表影子向左。
- $1\leq N, Q \leq 200000$
- $-10^ {18} \leq x_i \leq 10^ {18}$
- $x_i$ 兩兩相異
- $1 \leq h_i \leq 10^ 9$
- $-10^ 9 \leq q_i \leq 10^ 9$
Output Format
輸出一行,包含 $Q$ 個用空格分隔的整數。第 $i$ 個數字表示對應第 $i$ 個實驗中,根據給定的影子與木棍長度比值計算出的影子總長度。
Sample Input 1
3 4 1 5 15 2 3 4 -3 -2 2 4
Sample Output 1
20 16 18 30
Sample Input 2
5 6 1 5 11 19 26 2 2 7 2 3 -5 -4 -2 0 3 4
Sample Output 2
50 43 24 0 34 38
Hints
在第一個範例測資中,第一筆詢問的 $q_i$ 值為 -3,代表著影子的長度為棍子長度的 3 倍,影子向左。
棍子 1 會產生影子覆蓋到 $[-5, 1]$ 的範圍,棍子 2 會產生影子覆蓋到 $[-4, 5]$ 的範圍,棍子 3 會產生影子覆蓋到 $[3, 15]$ 的範圍,總共覆蓋到的範圍是 $[-5, 15]$,所以影子長度是 20。
第三筆詢問的 $q_i$ 值為 2,代表著影子的長度為棍子長度的 2 倍,影子向右。
棍子 1 會產生影子覆蓋到 $[1, 5]$ 的範圍,棍子 2 會產生影子覆蓋到 $[5, 11]$ 的範圍,棍子 3 會產生影子覆蓋到 $[15, 23]$ 的範圍,總共覆蓋到的範圍是 $[1, 11] \bigcup [15, 23]$,所以影子長度是 18。
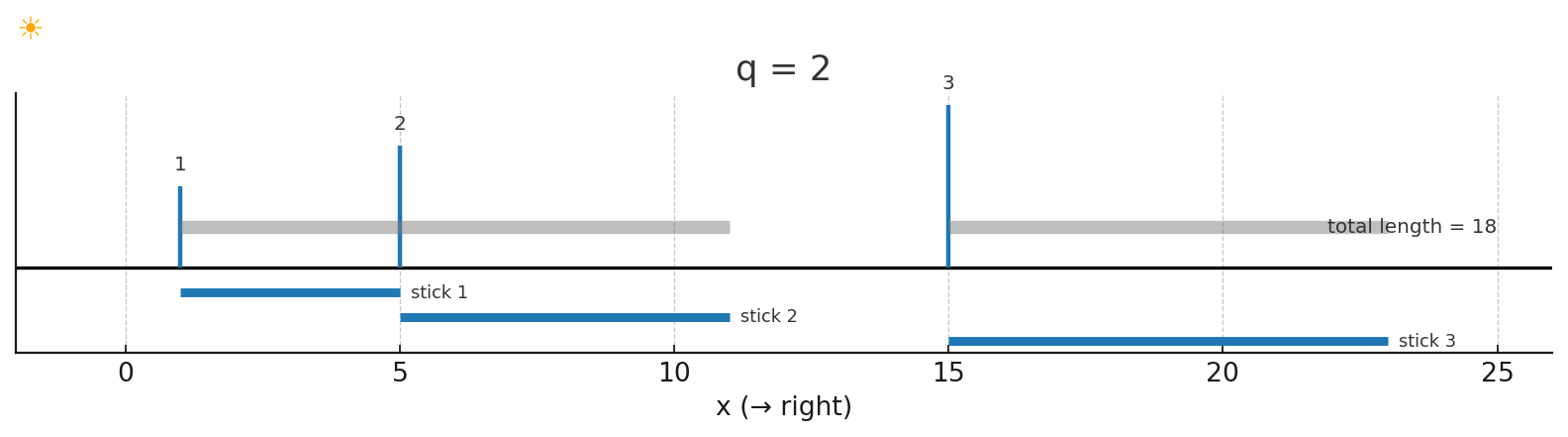
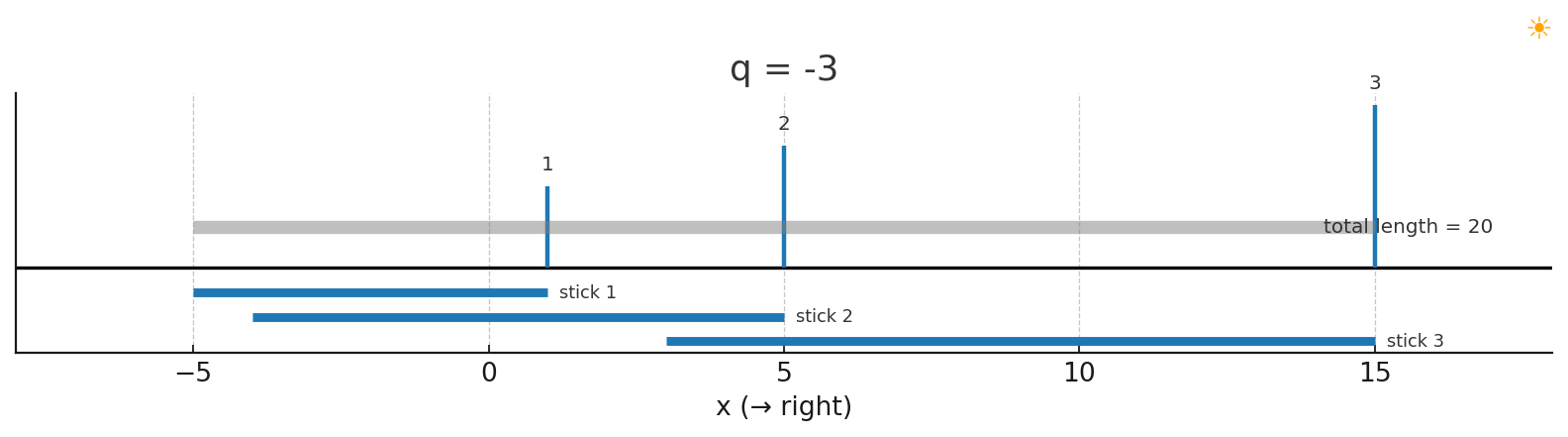
藍色的線為每根棍子產生的影子,灰色為聯集起來的範圍
Problem Source
YTP 2025 國中組程式挑戰營 p13
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~1 | 範例測試資料 | 0 |
| 2 | 2~61 | $N, Q \leq 2000$ | 10 |
| 3 | 0~125 | 無額外限制 | 15 |
