984 . 花咲川學園祭
TopCoder
Tags
Description
前情提要:請參考題目「狹路相逢勇者勝」。
偷摸林事務所(Tomorin プロダクション)第十屆培訓營的小石頭們方才於「狹路相逢」道館打出了一場氣勢如虹的勝仗。眾人正沉醉在慶功宴的歡笑與喧囂之中,然而椎名立希與八幡海鈴卻早已悄悄離席,循著蛛絲馬跡一路追蹤著事務所的吉祥物——那隻自由不羈的抹茶貓——要樂奈。最終,他們的追逐在花咲川學園的中庭畫下了新篇章。
此刻的花咲川中庭,正因學園祭而熱鬧非凡。整個場地可以抽象成一張圖:共有 $n$ 個位置與若干條道路交織。道路兩旁攤位林立,女僕咖啡廳的招呼聲、射水氣球的尖叫、鬼屋的驚呼與樂團的演奏交織成一片,但樂奈的眼裡卻只有攤位上琳瑯滿目的點心——這裡對她來說簡直就是天堂!
不過,樂奈對於路線有獨特的偏好:
- 當她身處於位置 $i$($1 \le i \le n$),便會選擇一條點心類型為 $c_i$ 的道路前往 $u_i$,同時理所當然地獲得招待並吞下那份點心(每次經過該道路都會獲得一份點心)。
根據後勤部部長三角初華的情報,樂奈一路上吞食的點心種類若依序拼接,正好形成一條字串 $S$。然而樂奈的食量之驚人,使得 $S$ 的長度遠超常人記憶所能負荷,因此必須表達成滿足合法壓縮字串形式的字串 $T$。
合法壓縮字串 <compressed> 的定義如下(Backus–Naur 形式,BNF):
<alphabet> ::= "a" | "b" | ... | "z"
; 所有小寫英文字元
<firstdigit> ::= "1" | "2" | "3" | "4" | "5" | "6" | "7" | "8" | "9"
<digit> ::= "0" | <firstdigit>
<digits> ::= <digit>
| <digit> <digits>
<number> ::= <firstdigit>
| <firstdigit> <digits>
<compressed> ::= <alphabet>
| <compressed> <compressed>
| "(" <compressed> ")" <number>
或是更直觀地說:
- $c = \texttt{a}, \texttt{b}, \ldots, \texttt{z}$(小寫英文字元)
- $v = \texttt{1}, \texttt{2}, \texttt{3}, \ldots$(不含前導 $0$ 的正整數)
- $E = c \mid EE \mid \texttt{(} \; E \; \texttt{)} \; v$
- $E$ 即為合法壓縮字串
其中,$\texttt{(} \; E \; \texttt{)} \; v$ 代表「將 $E$ 重複拼接 $v$ 遍」。舉例來說:
- $\texttt{(xyz)3}$ 解壓縮之後會變成 $\texttt{xyzxyzxyz}$;
- $\texttt{(ab)2(c(d)3)2}$ 解壓縮之後會變成 $\texttt{ababcdddcddd}$。
然而真正的難題在於:沒有人知道樂奈究竟從哪個位置啟程。作為花咲川後援會會長的小綠,你決定挺身而出。對於每一個可能的出發點 $i = 1, 2, \ldots, n$,定義從 $i$ 出發,走過 $|S|$ 步途中所經過的點心種類所組成的字串為 $W_i$。你的任務,是要判斷每一個 $W_i$ 與字串 $S$ 的大小關係。
Input Format
- line $1$: $\;\; n$
- line $2$: $\;\; u_1 \;\; u_2 \;\; \ldots \;\; u_n$
- line $3$: $\;\; c_1 \;\; c_2 \;\; \ldots \;\; c_n$
- line $4$: $\;\; T$
資料範圍:
- $1 \le n \le 10\,000$。
- $1 \le u_i \le n$($1 \le i \le n$)。
- $c_i$ 是小寫英文字母($1 \le i \le n$)。
- $1 \le |T| \le 500$。
- 字串 $T$ 中的字元 $c$ 是小寫英文字母。
- $1 \le$ 字串 $T$ 中的數字 $v$ $\le 10^ 9$。
Output Format
- line $1$: $\;\; \text{cmp}_1 \text{cmp}_2 \ldots \text{cmp}_n \;\;$(不含空格)
- 令從 $i$ 出發走 $|S|$ 步會得到字串 $W_i$,則 $\text{cmp}_i$ 為使 $W_i \ \square\ S$ 成立時在 $\square$ 中填入的字元(
<、=、>)。
- 令從 $i$ 出發走 $|S|$ 步會得到字串 $W_i$,則 $\text{cmp}_i$ 為使 $W_i \ \square\ S$ 成立時在 $\square$ 中填入的字元(
Sample Input 1
6 1 3 2 5 6 4 a a b a b a aabaa
Sample Output 1
<>>>>=
Sample Input 2
3 1 2 3 a b c (b)1000000000
Sample Output 2
<=>
Sample Input 3
5 3 1 4 1 5 p i z z a ((p(z)2)3((p)1zz)9)7p
Sample Output 3
=<>><
Hints
範例一
該輸入滿足所有子任務的限制。
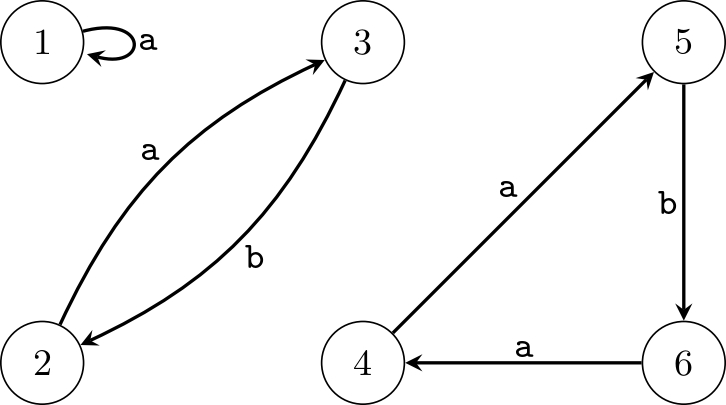
要樂奈從每個位置出發,行經五條道路上的字元拼接而成的字串 $W_i$($1 \le i \le 6$)分別為:
- $W_1 = \texttt{aaaaa < aabaa} = S$
- $W_2 = \texttt{ababa > aabaa} = S$
- $W_3 = \texttt{babab > aabaa} = S$
- $W_4 = \texttt{abaab > aabaa} = S$
- $W_5 = \texttt{baaba > aabaa} = S$
- $W_6 = \texttt{aabaa = aabaa} = S$
範例二
該輸入滿足子任務 2, 4 的限制。
- $W_1 = \texttt{(a)1000000000 < (b)1000000000} = S$
- $W_2 = \texttt{(b)1000000000 = (b)1000000000} = S$
- $W_3 = \texttt{(c)1000000000 > (b)1000000000} = S$
範例三
該輸入滿足子任務 3, 4 的限制。
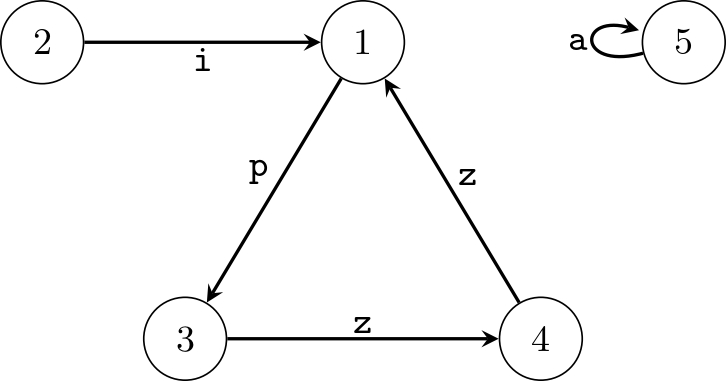
Problem Source
YTP 2025 國中組程式挑戰營 p14
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 36~38 | 範例測試資料。 | 0 |
| 2 | 0~3, 36 | $T$ 只會由第一、二種方法構造出來,也就是說不存在括弧。 | 3 |
| 3 | 0~11, 36~37 | $T$ 由第三種構造方法中的 $E$ 只會由第一、二種方法構造出來,也就是說不存在括弧套括弧。 | 6 |
| 4 | 0~3, 12~23, 36, 38 | 字串 $T$ 中的數字 $v$ $\le 9$。 | 6 |
| 5 | 0~38 | 無額外限制。 | 10 |
