985 . 邊框反轉
TopCoder
Tags
Description
有一個 $n \times m$ 的表格,我們稱第 $i$ 個橫列跟第 $j$ 個直排的交集格子為 $(i, j)$。對於每一個格子 $(i, j)$,裡面會有一片葉子或是一個硬幣。
小里子可以發動忍術,對這表格進行以下操作任意多次:
- 先挑選一個大於等於 2 的正整數 $k$ 與一個大小為 $k \times k$ 的子方陣,接著對於所有位於此子方陣邊界的格子,若該格子原本放著葉子,就將它變成硬幣,否則將它變成葉子。
- 更具體來說,挑選一個正整數 $k \geq 2$ 與一個滿足 $x + k - 1 \leq n, y + k - 1 \leq m$ 的格子 $(x, y)$,將所有滿足至少一個以下條件的格子 $(x', y')$ 改變狀態(葉子變硬幣或硬幣變葉子)。
- $x' = x$ 且 $y \leq y' \leq y + k - 1$
- $x' = x + k - 1$ 且 $y \leq y' \leq y + k - 1$
- $y' = y$ 且 $x \leq x' \leq x + k - 1$
- $y' = y + k - 1$ 且 $x \leq x' \leq x + k - 1$
小里子喜歡葉子,她希望能將所有格子都變成葉子,但她又不希望施展太多次忍術,她最多只想使用 $5nm$ 次。請幫她判斷能不能完成目標,如果可以的話也幫她構造出一組合法的操作。
Input Format
輸入第一行有一個正整數 $t$,代表測資的數量。
對於每筆測資,第一行有兩個正整數 $n, m$,代表表格的大小。
接下來 $n$ 行,每行有一個長度為 $m$ 的 01 字串 $s_i$。若 $s_i$ 的第 $j$ 個字元為 0,則代表一開始格子 $(i, j)$ 放著葉子,若為 1 則代表放著硬幣。
- $1 \leq t \leq 10000$
- $2 \leq n, m \leq 300$
- $|s_i| = m$
- $s_{i, j} \in \lbrace 0, 1 \rbrace$
- $n \times m$ 的總和不超過 $10^ 5$
Output Format
對於每筆測資,若該筆測資無法達成目標,請輸出恰一行 -1。
否則請在第一行輸出一個整數 $q$ 代表操作的數量。接下來 $q$ 行,每行輸出三個正整數 $x, y, k$ 代表第 $i$ 筆操作選擇了 $(x, y)$ 作為子方陣的左上角,且方陣大小為 $k \times k$。請注意你不用最小化操作數量,你的答案會被視為正確若滿足以下所有條件:
- $0 \leq q \leq 5nm$
- 對於所有操作,格子 $(x, y)$ 與 $(x + k - 1, y + k - 1)$ 皆在表格範圍內且 $k \geq 2$。
- 完成所有操作後,所有的格子都是葉子。
Sample Input 1
4 5 6 100011 110101 110101 100001 010011 3 3 010 101 010 2 2 01 10 2 2 00 00
Sample Output 1
3 1 1 4 1 2 5 4 3 2 5 1 1 3 1 1 2 2 1 2 1 2 2 2 2 2 -1 0
Hints
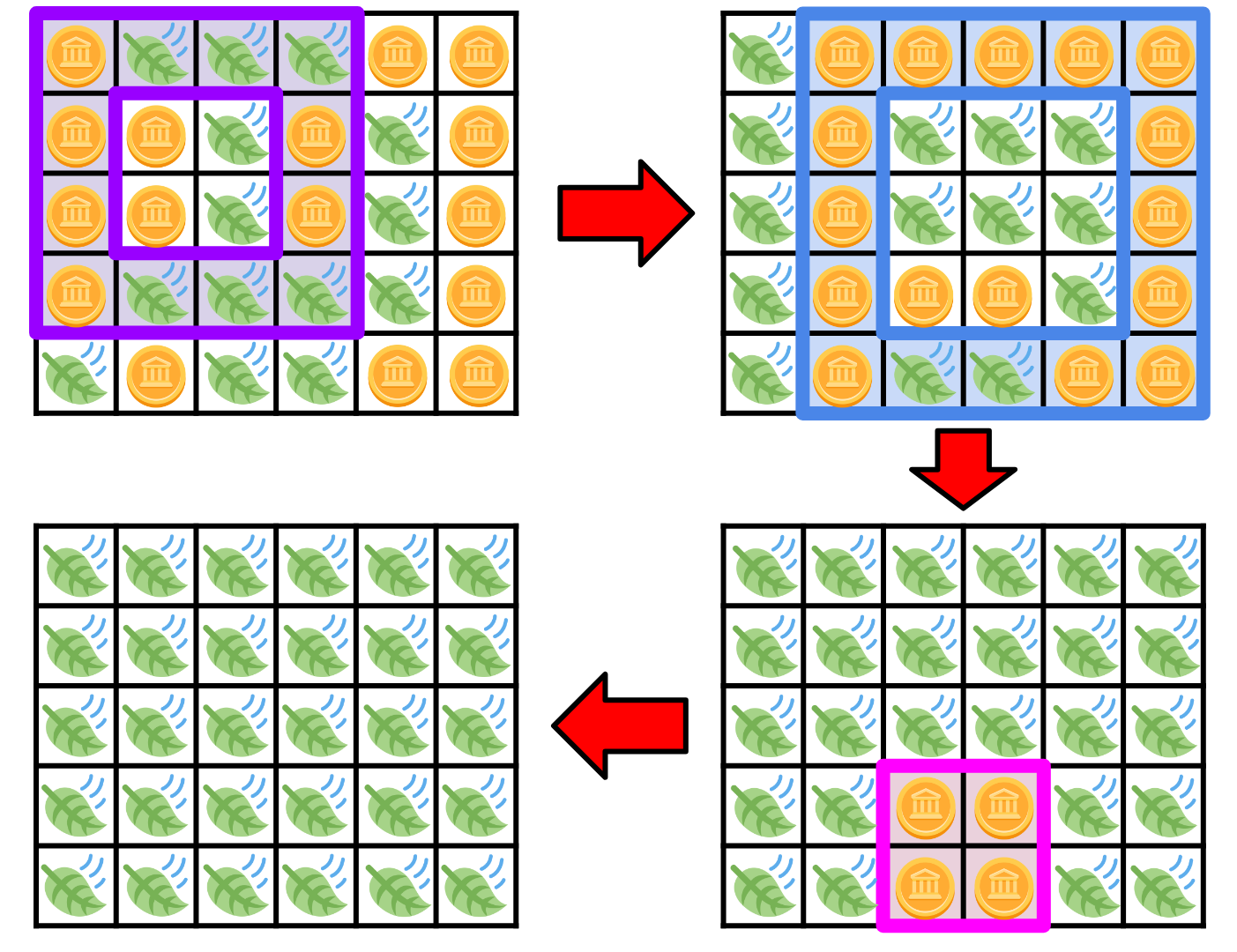
下圖說明了範例測資一依序進行的操作與對應的結果。
Problem Source
YTP 2025 國中組程式挑戰營 p15
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0 | 範例測試資料 | 0 |
| 2 | 1~10 | $n = 2$ | 3 |
| 3 | 0~60 | 無額外限制 | 22 |
